| << Chapter < Page | Chapter >> Page > |
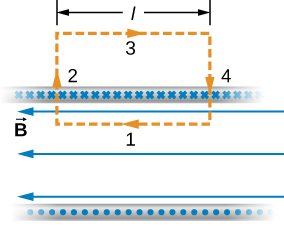
The solenoid has n turns per unit length, so the current that passes through the surface enclosed by the path is nlI . Therefore, from Ampère’s law,
and
within the solenoid. This agrees with what we found earlier for B on the central axis of the solenoid. Here, however, the location of segment 1 is arbitrary, so we have found that this equation gives the magnetic field everywhere inside the infinite solenoid.
Outside the solenoid, one can draw an Ampère’s law loop around the entire solenoid. This would enclose current flowing in both directions. Therefore, the net current inside the loop is zero. According to Ampère’s law, if the net current is zero, the magnetic field must be zero. Therefore, for locations outside of the solenoid’s radius, the magnetic field is zero.
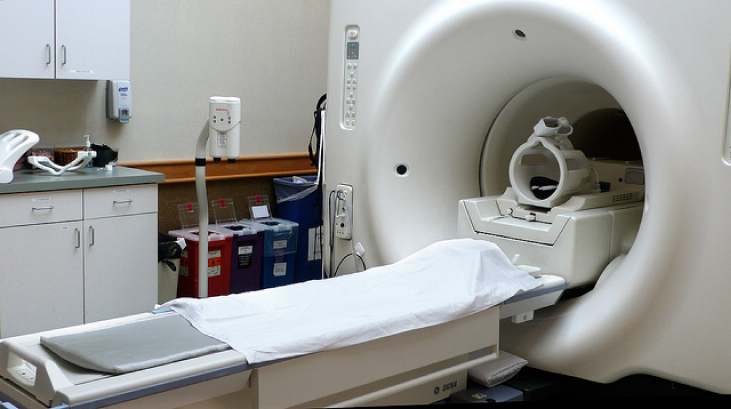
When a patient undergoes a magnetic resonance imaging (MRI) scan, the person lies down on a table that is moved into the center of a large solenoid that can generate very large magnetic fields. The solenoid is capable of these high fields from high currents flowing through superconducting wires. The large magnetic field is used to change the spin of protons in the patient’s body. The time it takes for the spins to align or relax (return to original orientation) is a signature of different tissues that can be analyzed to see if the structures of the tissues is normal ( [link] ).
The magnetic field produced inside the solenoid is
Check Your Understanding What is the ratio of the magnetic field produced from using a finite formula over the infinite approximation for an angle of (a) (b) The solenoid has 1000 turns in 50 cm with a current of 1.0 A flowing through the coils
a. 1.00382; b. 1.00015
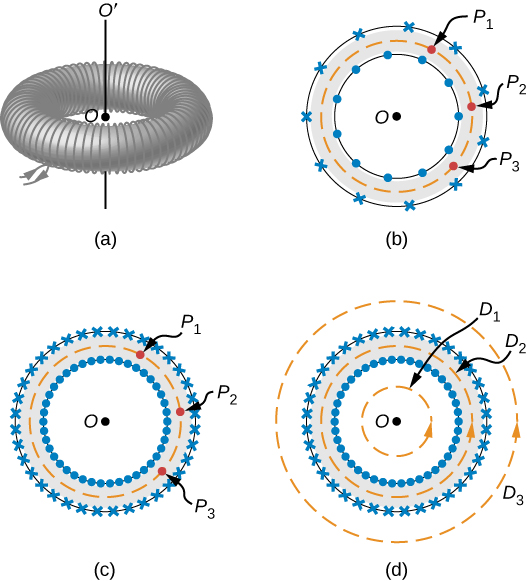
A toroid is a donut-shaped coil closely wound with one continuous wire, as illustrated in part (a) of [link] . If the toroid has N windings and the current in the wire is I , what is the magnetic field both inside and outside the toroid?

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?