| << Chapter < Page | Chapter >> Page > |
Polygons are closed figures with three or more straight sides. If all the sides are the same length, and all the internal angles are equal, we call them regul a r polygons. Triangles are three-sided polygons, and an equil a ter a l triangle is a regul a r three-sided polygon. A square is a regular four-sided polygon. Pent agons have five sides, hexagons have six sides and heptagons have seven. Make a list of as many of these special names as you can find.
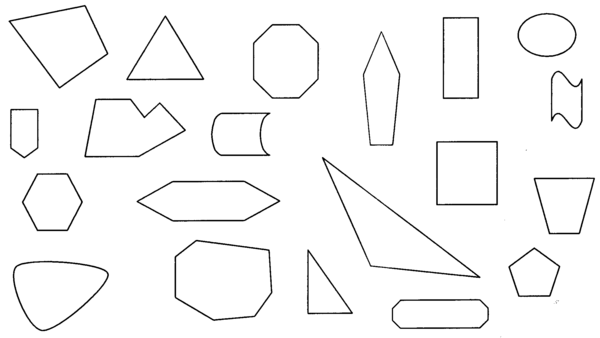
Here are several closed plane figures. Decorate them and write the name of each polygon on the shape.
B. Investig a tion
Choose four polygons from the group above, all regular, but with four different numbers of sides. Now measure the sizes of the internal angles of each. Try to find out whether it is possible to make a formula to tell you how large the angles are, and what they add up to.
The following table will be helpful. As you can see, there are infinitely many polygons.
| No. of sides | a = internal angle size | b = 360 – a | c = b – 180 | Total of a | Total of c |
| Three | 3× a = | 3× c = | |||
| Four | 4× a = | 4× c = | |||
| Five | 5× a = | 5× c = | |||
| Six | 6× a = | 6× c = | |||
| Seven | 7× a = | 7× c = | |||
| Twelve | 12× a = | 12× c = |
C. Three-dimension a l closed figures
D. Project
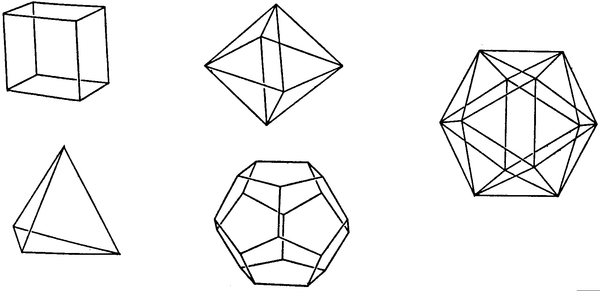
Research the five Platonic Solids, finding their names and properties, and other interesting deductions and facts about them. Make an attractive poster or models of these solids showing the facts associated with each. Below are pictures of the five solids.
| LO 3 |
| Space and Shape (Geometry)The learner will be able to describe and represent characteristics and relationships between two-dimensional shapes and three-dimensional objects in a variety of orientations and positions. |
| We know this when the learner : |
| 3.1 recognises, visualises and names geometric figures and solids in natural and cultural forms and geometric settings, including:3.1.1 regular and irregular polygons and polyhedra;3.1.2 spheres;3.1.3 cylinders;3.2 in contexts that include those that may be used to build awareness of social, cultural and environmental issues, describes the interrelationships of the properties of geometric figures and solids with justification, including:3.2.1 congruence and straight line geometry;3.3 uses geometry of straight lines and triangles to solve problems and to justify relationships in geometric figures;3.4 draws and/or constructs geometric figures and makes models of solids in order to investigate and compare their properties and model situations in the environment; |
| 3.5 uses transformations, congruence and similarity to investigate, describe and justify (alone and/or as a member of a group or team) properties of geometric figures and solids, including tests for similarity and congruence of triangles. |
Discussion
Solutions – exercise:
Rectangular prism: TBO = 412 cm 2 Vol = 480 cm 3
Triangular prism: TBO = 307,71 cm 2 Vol = 360 cm 3
Cylinder: TBO = 402,12 cm 2 Vol = 603,19 cm 3
Granny’s Jam Pot: Vol = 8 595,40 cm 2
11 Square–based jars: Vol = 8 096 cm 2
11 Rectangle–based jars: Vol =8 633,63 cm 2
So, granny must use the rectangular–based jars if she wants to fit all the jam in!
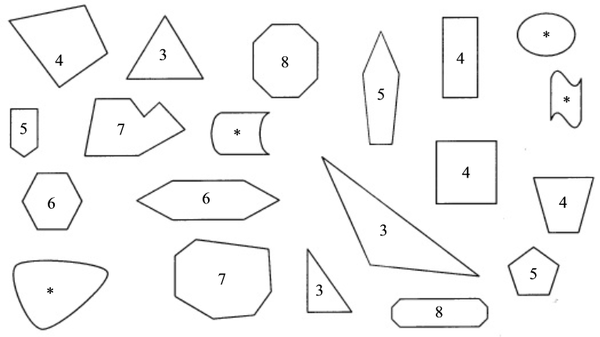
3 = triangle; 4 = tetragon; 5 = pentagon; 6 = hexagon; 7 = heptagon; 8 = octagon; * = not polygon
| No of sides | a = internal angle size | b = 360° – a | c = b – 180° | Total of a | Total of c |
| Three | 60° | 300° | 120° | 3× a = 180° | 3× c = 360° |
| Four | 90° | 270° | 90° | 4× a = 360° | 4× c = 360° |
| Five | 108° | 252° | 72° | 5× a = 540° | 5× c = 360° |
| Six | 120° | 240° | 60° | 6× a = 720° | 6× c = 360° |
| Seven | 308,57° | 51,43° | –128,57° | 7× a = 2160° | 7× c = –360° |
| Twelve | 330° | 30° | –150° | 12× a = 3960° | 12× c = –360° |
TEST 1
1. Explain how you would recognise a right prism.
2. Explain how you could find the base of a right prism.
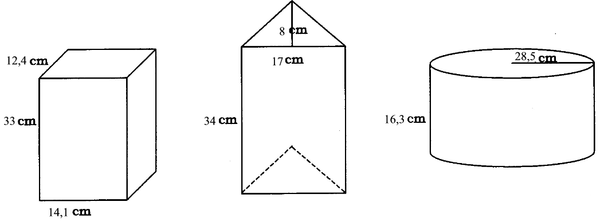
3. Calculate the total surface area and the volume of each of the following three prisms. Give your answers accurate to two decimal places.
TEST 1 – Memorandum
1. Essential points in the explanation: three-dimensional; top and base congruent plane shapes; side(s) at right angles to base.
2. Any reasonable explanation, e.g. if the chosen side is placed at the bottom, the description of a right prism fits what you see.
3. Rectangular right prism: TBO = 1 939,68 cm 2 Volume = 5 769,72 cm 3
Triangular right prism: TBO = 1 507,74 mm 2 Volume = 2 312 mm 3
Cylinder: TBO = 8 022,37 m 2 Volume = 41 593,67 m 3

Notification Switch
Would you like to follow the 'Mathematics grade 9' conversation and receive update notifications?