7.2 Right triangle trigonometry  (Page 3/12)

Using equal cofunction of complements

If we look more closely at the relationship between the sine and cosine of the special angles, we notice a pattern. In a right triangle with angles of $\frac{\pi }{6}$ and $\frac{\pi }{3},$ we see that the sine of $\frac{\pi }{3},$ namely $\frac{\sqrt{3}}{2},$ is also the cosine of $\frac{\pi }{6},$ while the sine of $\frac{\pi }{6},$ namely $\frac{1}{2},$ is also the cosine of $\frac{\pi }{3}.$

See [link] .

This result should not be surprising because, as we see from [link] , the side opposite the angle of $\frac{\pi }{3}$ is also the side adjacent to $\frac{\pi }{6},$ so $\sin \left(\frac{\pi }{3}\right)$ and $\cos \left(\frac{\pi }{6}\right)$ are exactly the same ratio of the same two sides, $\sqrt{3}s$ and $2s.$ Similarly, $\cos \left(\frac{\pi }{3}\right)$ and $\sin \left(\frac{\pi }{6}\right)$ are also the same ratio using the same two sides, $s$ and $2s.$

The interrelationship between the sines and cosines of $\frac{\pi }{6}$ and $\frac{\pi }{3}$ also holds for the two acute angles in any right triangle, since in every case, the ratio of the same two sides would constitute the sine of one angle and the cosine of the other. Since the three angles of a triangle add to $\pi ,$ and the right angle is $\frac{\pi }{2},$ the remaining two angles must also add up to $\frac{\pi }{2}.$ That means that a right triangle can be formed with any two angles that add to $\frac{\pi }{2}$ —in other words, any two complementary angles. So we may state a cofunction identity : If any two angles are complementary, the sine of one is the cosine of the other, and vice versa. This identity is illustrated in [link] .

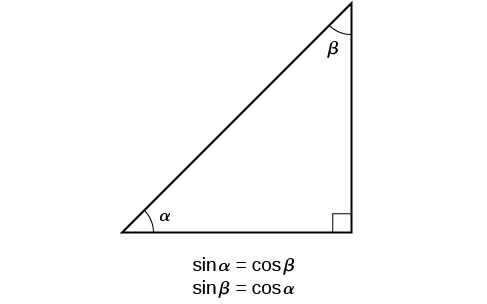
Using this identity, we can state without calculating, for instance, that the sine of $\frac{\pi }{12}$ equals the cosine of $\frac{5\pi }{12},$ and that the sine of $\frac{5\pi }{12}$ equals the cosine of $\frac{\pi }{12}.$ We can also state that if, for a given angle $t,\cos t=\frac{5}{13},$ then $\sin \left(\frac{\pi }{2}-t\right)=\frac{5}{13}$ as well.

Using trigonometric functions

In previous examples, we evaluated the sine and cosine in triangles where we knew all three sides. But the real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides.