0.1 Proofs, identities, and toolkit functions

<< Chapter < Page

Algebra and trigonometry Page 1 / 1

Chapter >> Page >

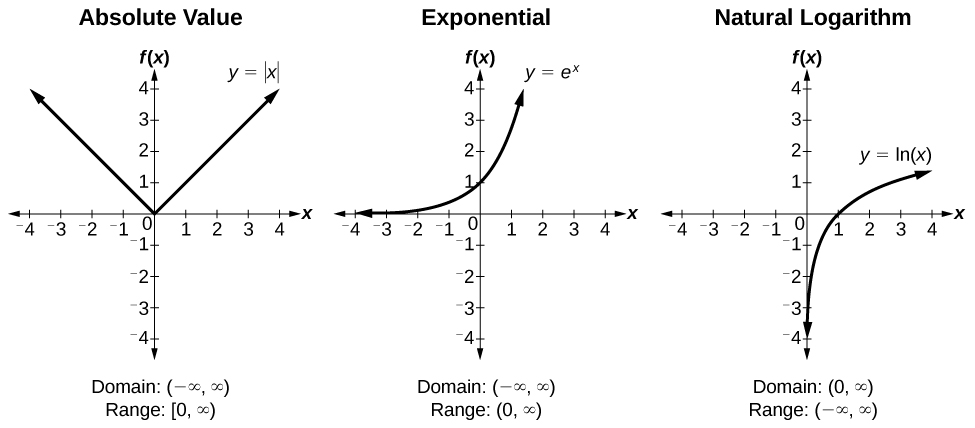
Appendix

Important proofs and derivations

Product Rule

$\log_{a} x y = \log_{a} x + \log_{a} y$

Proof:

Let $m = \log_{a} x$ and $n = \log_{a} y .$

Write in exponent form.

$x = a^{m}$ and $y = a^{n} .$

Multiply.

$x y = a^{m} a^{n} = a^{m + n}$

$\begin{matrix} a^{m + n} & = & x y \\ \log_{a} (x y) & = & m + n \\ = & \log_{a} x + \log_{b} y \end{matrix}$

Change of Base Rule

$\begin{array}{l} \log_{a} b = \frac{\log_{c} b}{\log_{c} a} \\ \log_{a} b = \frac{1}{\log_{b} a} \end{array}$

where $x$ and $y$ are positive, and $a > 0, a \neq 1.$

Proof:

Let $x = \log_{a} b .$

Write in exponent form.

$a^{x} = b$

Take the $\log_{c}$ of both sides.

$\begin{matrix} \log_{c} a^{x} & = & \log_{c} b \\ x \log_{c} a & = & \log_{c} b \\ x & = & \frac{\log_{c} b}{\log_{c} a} \\ \log_{a} b & = & \frac{\log_{c} b}{\log_{a} b} \end{matrix}$

When $c = b,$

$\log_{a} b = \frac{\log_{b} b}{\log_{b} a} = \frac{1}{\log_{b} a}$

Heron’s Formula

$A = \sqrt{s (s - a) (s - b) (s - c)}$

where $s = \frac{a + b + c}{2}$

Proof:

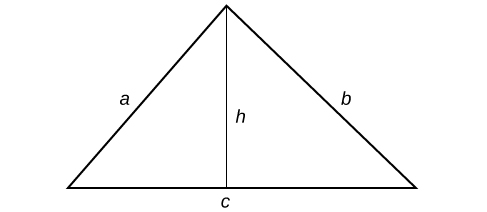
Let $a,$ $b,$ and $c$ be the sides of a triangle, and $h$ be the height.

A triangle with sides labeled: a, b and c. A line runs through the center of the triangle, bisecting the top angle; this line is labeled: h.

So $s = \frac{a + b + c}{2}$ .

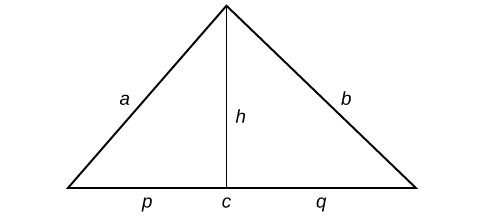
We can further name the parts of the base in each triangle established by the height such that $p + q = c .$

A triangle with sides labeled: a, b, and c. A line runs through the center of the triangle bisecting the angle at the top; this line is labeled: h. The two new line segments on the base of the triangle are labeled: p and q.

Using the Pythagorean Theorem, $h^{2} + p^{2} = a^{2}$ and $h^{2} + q^{2} = b^{2} .$

Since $q = c - p,$ then $q^{2} = {(c - p)}^{2} .$ Expanding, we find that $q^{2} = c^{2} - 2 c p + p^{2} .$

We can then add $h^{2}$ to each side of the equation to get $h^{2} + q^{2} = h^{2} + c^{2} - 2 c p + p^{2} .$

Substitute this result into the equation $h^{2} + q^{2} = b^{2}$ yields $b^{2} = h^{2} + c^{2} - 2 c p + p^{2} .$

Then replacing $h^{2} + p^{2}$ with $a^{2}$ gives $b^{2} = a^{2} - 2 c p + c^{2} .$

Solve for $p$ to get

$p = \frac{a^{2} + b^{2} - c^{2}}{2 c}$

Since $h^{2} = a^{2} - p^{2},$ we get an expression in terms of $a,$ $b,$ and $c .$

$\begin{matrix} h^{2} & = & a^{2} - p^{2} \\ = & (a + p) (a - p) \\ = & [a + \frac{(a^{2} + c^{2} - b^{2})}{2 c}] [a - \frac{(a^{2} + c^{2} - b^{2})}{2 c}] \\ = & \frac{(2 a c + a^{2} + c^{2} - b^{2}) (2 a c - a^{2} - c^{2} + b^{2})}{4 c^{2}} \\ = & \frac{({(a + c)}^{2} - b^{2}) (b^{2} - {(a - c)}^{2})}{4 c^{2}} \\ = & \frac{(a + b + c) (a + c - b) (b + a - c) (b - a + c)}{4 c^{2}} \\ = & \frac{(a + b + c) (- a + b + c) (a - b + c) (a + b - c)}{4 c^{2}} \\ = & \frac{2 s \cdot (2 s - a) \cdot (2 s - b) (2 s - c)}{4 c^{2}} \end{matrix}$

Therefore,

$\begin{matrix} h^{2} & = & \frac{4 s (s - a) (s - b) (s - c)}{c^{2}} \\ h & = & \frac{2 \sqrt{s (s - a) (s - b) (s - c)}}{c} \end{matrix}$

And since $A = \frac{1}{2} c h,$ then

$\begin{matrix} A & = & \frac{1}{2} c \frac{2 \sqrt{s (s - a) (s - b) (s - c)}}{c} \\ = & \sqrt{s (s - a) (s - b) (s - c)} \end{matrix}$

Properties of the Dot Product

$u \cdot v = v \cdot u$

Proof:

$\begin{matrix} u \cdot v & = ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \cdot ⟨ v_{1}, v_{2}, ... v_{n} ⟩ \\ = u_{1} v_{1} + u_{2} v_{2} + ... + u_{n} v_{n} \\ = v_{1} u_{1} + v_{2} u_{2} + ... + v_{n} v_{n} \\ = ⟨ v_{1}, v_{2}, ... v_{n} ⟩ \cdot ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \\ = v \cdot u \end{matrix}$

$u \cdot (v + w) = u \cdot v + u \cdot w$

Proof:

$\begin{matrix} u \cdot (v + w) & = ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \cdot (⟨ v_{1}, v_{2}, ... v_{n} ⟩ + ⟨ w_{1}, w_{2}, ... w_{n} ⟩) \\ = ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \cdot ⟨ v_{1} + w_{1}, v_{2} + w_{2}, ... v_{n} + w_{n} ⟩ \\ = ⟨ u_{1} (v_{1} + w_{1}), u_{2} (v_{2} + w_{2}), ... u_{n} (v_{n} + w_{n}) ⟩ \\ = ⟨ u_{1} v_{1} + u_{1} w_{1}, u_{2} v_{2} + u_{2} w_{2}, ... u_{n} v_{n} + u_{n} w_{n} ⟩ \\ = ⟨ u_{1} v_{1}, u_{2} v_{2}, ..., u_{n} v_{n} ⟩ + ⟨ u_{1} w_{1}, u_{2} w_{2}, ..., u_{n} w_{n} ⟩ \\ = ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \cdot ⟨ v_{1}, v_{2}, ... v_{n} ⟩ + ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \cdot ⟨ w_{1}, w_{2}, ... w_{n} ⟩ \\ = u \cdot v + u \cdot w \end{matrix}$

$u \cdot u = {| u |}^{2}$

Proof:

$\begin{matrix} u \cdot u & = ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \cdot ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \\ = u_{1} u_{1} + u_{2} u_{2} + ... + u_{n} u_{n} \\ = u_{1}^{2} + u_{2}^{2} + ... + u_{n}^{2} \\ = | ⟨ u_{1}, u_{2}, ... u_{n} ⟩ |^{2} \\ = v \cdot u \end{matrix}$

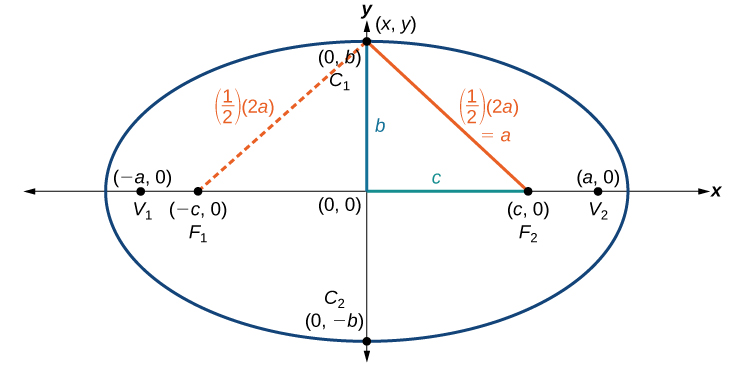
Standard Form of the Ellipse centered at the Origin

$1 = \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$

Derivation

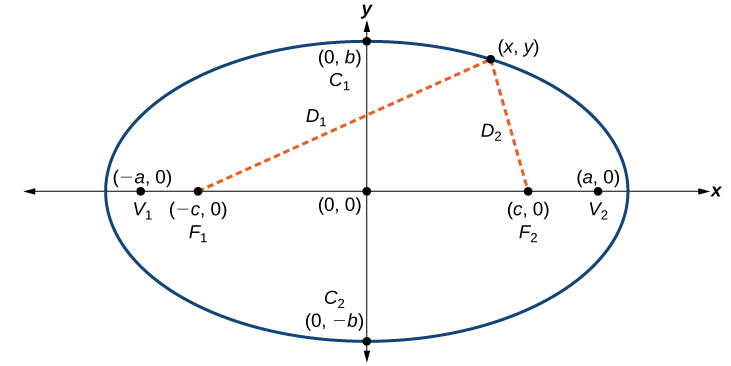
An ellipse consists of all the points for which the sum of distances from two foci is constant:

$\sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} + \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} = constant$

An ellipse centered at the origin on an x, y-coordinate plane. Points C1 and C2 are plotted at the points (0, b) and (0, -b) respectively; these points appear on the ellipse. Points V1 and V2 are plotted at the points (-a, 0) and (a, 0) respectively; these points appear on the ellipse. Points F1 and F2 are plotted at the points (-c, 0) and (c, 0) respectively; these points appear on the x-axis, but not the ellipse. The point (x, y) appears on the ellipse in the first quadrant. Dotted lines extend from F1 and F2 to the point (x, y).

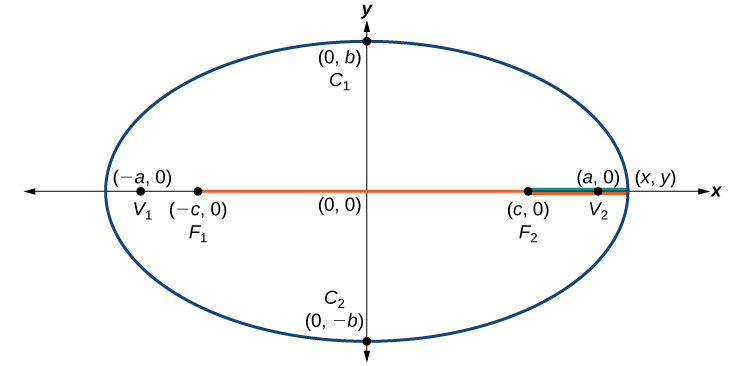
Consider a vertex.

An ellipse centered at the origin. The points C1 and C2 are plotted at the points (0, b) and (0, -b) respectively; these points are on the ellipse. The points V1 and V2 are plotted at the points (-a, 0) and (a, 0) respectively; these points are on the ellipse. The points F1 and F2 are plotted at the points (-c, 0) and (c, 0) respectively; these points are on the x-axis and not on the ellipse. A line extends from the point F1 to a point (x, y) which is at the point (a, 0). A line extends from the point F2 to the point (x, y) as well.

Then, $\sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} + \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} = 2 a$

Consider a covertex.

Then $b^{2} + c^{2} = a^{2} .$

$\begin{matrix} \sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} + \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} & = & 2 a \\ \sqrt{{(x + c)}^{2} + y^{2}} & = & 2 a - \sqrt{{(x - c)}^{2} + y^{2}} \\ {(x + c)}^{2} + y^{2} & = & {(2 a - \sqrt{{(x - c)}^{2} + y^{2}})}^{2} \\ x^{2} + 2 c x + c^{2} + y^{2} & = & 4 a^{2} - 4 a \sqrt{{(x - c)}^{2} + y^{2}} + {(x - c)}^{2} + y^{2} \\ x^{2} + 2 c x + c^{2} + y^{2} & = & 4 a^{2} - 4 a \sqrt{{(x - c)}^{2} + y^{2}} + x^{2} - 2 c x + y^{2} \\ 2 c x & = & 4 a^{2} - 4 a \sqrt{{(x - c)}^{2} + y^{2}} - 2 c x \\ 4 c x - 4 a^{2} & = & 4 a \sqrt{{(x - c)}^{2} + y^{2}} \\ - \frac{1}{4 a} (4 c x - 4 a^{2}) & = & \sqrt{{(x - c)}^{2} + y^{2}} \\ a - \frac{c}{a} x & = & \sqrt{{(x - c)}^{2} + y^{2}} \\ a^{2} - 2 x c + \frac{c^{2}}{a^{2}} x^{2} & = & {(x - c)}^{2} + y^{2} \\ a^{2} - 2 x c + \frac{c^{2}}{a^{2}} x^{2} & = & x^{2} - 2 x c + c^{2} + y^{2} \\ a^{2} + \frac{c^{2}}{a^{2}} x^{2} & = & x^{2} + c^{2} + y^{2} \\ a^{2} + \frac{c^{2}}{a^{2}} x^{2} & = & x^{2} + c^{2} + y^{2} \\ a^{2} - c^{2} & = & x^{2} - \frac{c^{2}}{a^{2}} x^{2} + y^{2} \\ a^{2} - c^{2} & = & x^{2} (1 - \frac{c^{2}}{a^{2}}) + y^{2} \end{matrix}$

Let $1 = \frac{a^{2}}{a^{2}} .$

\begin{matrix} a^{2} - c^{2} & = & x^{2} (\frac{a^{2} - c^{2}}{a^{2}}) + y^{2} \\ 1 & = & \frac{x^{2}}{a^{2}} + \frac{y^{2}}{a^{2} - c^{2}} \end{matrix}

Because $b^{2} + c^{2} = a^{2},$ then $b^{2} = a^{2} - c^{2} .$

\begin{matrix} 1 & = & \frac{x^{2}}{a^{2}} + \frac{y^{2}}{a^{2} - c^{2}} \\ 1 & = & \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} \end{matrix}

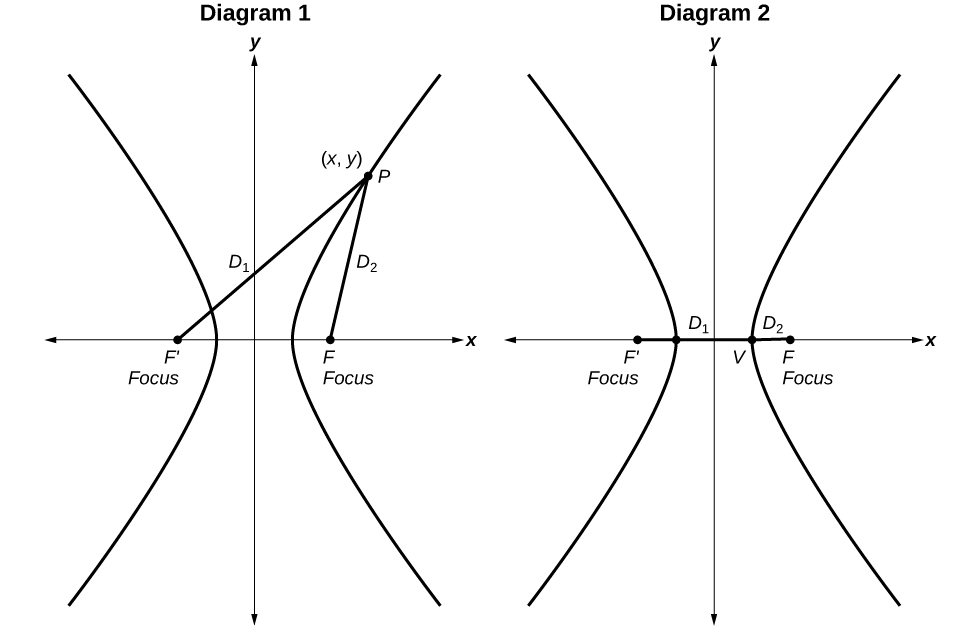
Standard Form of the Hyperbola

$1 = \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}}$

Derivation

A hyperbola is the set of all points in a plane such that the absolute value of the difference of the distances between two fixed points is constant.

Side-by-side graphs of hyperbole. In Diagram 1: The foci F’ and F are labeled and can be found a little in front of the opening of the hyperbola. A point P at (x,y) on the right curve is labeled. A line extends from the F’ focus to the point P labeled: D1. A line extends from the F focus to the point P labeled: D2. In Diagram 2: The foci F’ and F are labeled and can be found a little in front of the opening of the hyperbola. A point V is labeled at the vertex of the right hyperbola. A line extends from the F’ focus to the point V labeled: D1. A line extends from the F focus to the point V labeled: D2.

Diagram 1: The difference of the distances from Point P to the foci is constant:

$\sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} - \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} = constant$

Diagram 2: When the point is a vertex, the difference is $2 a .$

$\sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} - \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} = 2 a$

$\begin{matrix} \sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} - \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} & = & 2 a \\ \sqrt{{(x + c)}^{2} + y^{2}} - \sqrt{{(x - c)}^{2} + y^{2}} & = & 2 a \\ \sqrt{{(x + c)}^{2} + y^{2}} & = & 2 a + \sqrt{{(x - c)}^{2} + y^{2}} \\ {(x + c)}^{2} + y^{2} & = & (2 a + \sqrt{{(x - c)}^{2} + y^{2}}) \\ x^{2} + 2 c x + c^{2} + y^{2} & = & 4 a^{2} + 4 a \sqrt{{(x - c)}^{2}} + y^{2} \\ x^{2} + 2 c x + c^{2} + y^{2} & = & 4 a^{2} + 4 a \sqrt{{(x - c)}^{2} + y^{2}} + x^{2} - 2 c x + y^{2} \\ 2 c x & = & 4 a^{2} + 4 a \sqrt{{(x - c)}^{2} + y^{2}} - 2 c x \\ 4 c x - 4 a^{2} & = & 4 a \sqrt{{(x - c)}^{2} + y^{2}} \\ c x - a^{2} & = & a \sqrt{{(x - c)}^{2} + y^{2}} \\ {(c x - a^{2})}^{2} & = & a^{2} ({(x - c)}^{2} + y^{2}) \\ c^{2} x^{2} - 2 a^{2} c^{2} x^{2} + a^{4} & = & a^{2} x^{2} - 2 a^{2} c^{2} x^{2} + a^{2} c^{2} + a^{2} y^{2} \\ c^{2} x^{2} + a^{4} & = & a^{2} x^{2} + a^{2} c^{2} + a^{2} y^{2} \\ a^{4} - a^{2} c^{2} & = & a^{2} x^{2} - c^{2} x^{2} + a^{2} y^{2} \\ a^{2} (a^{2} - c^{2}) & = & (a^{2} - c^{2}) x^{2} + a^{2} y^{2} \\ a^{2} (a^{2} - c^{2}) & = & (c^{2} - a^{2}) x^{2} - a^{2} y^{2} \end{matrix}$

Define $b$ as a positive number such that $b^{2} = c^{2} - a^{2} .$

\begin{matrix} a^{2} b^{2} & = & b^{2} x^{2} - a^{2} y^{2} \\ \frac{a^{2} b^{2}}{a^{2} b^{2}} & = & \frac{b^{2} x^{2}}{a^{2} b^{2}} - \frac{a^{2} y^{2}}{a^{2} b^{2}} \\ 1 & = & \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} \end{matrix}

Trigonometric identities

Pythagorean Identity	$\begin{array}{l} \cos^{2} t + \sin^{2} t = 1 \\ 1 + \tan^{2} t = \sec^{2} t \\ 1 + \cot^{2} t = \csc^{2} t \end{array}$
Even-Odd Identities	$\begin{array}{l} \cos (- t) = c o s t \\ \sec (- t) = \sec t \\ \sin (- t) = - \sin t \\ \tan (- t) = - \tan t \\ \csc (- t) = - \csc t \\ \cot (- t) = - \cot t \end{array}$
Cofunction Identities	$\begin{array}{l} \cos t = \sin (\frac{π}{2} - t) \\ \sin t = \cos (\frac{π}{2} - t) \\ \tan t = \cot (\frac{π}{2} - t) \\ \cot t = \tan (\frac{π}{2} - t) \\ \sec t = \csc (\frac{π}{2} - t) \\ \csc t = \sec (\frac{π}{2} - t) \end{array}$
Fundamental Identities	$\begin{array}{l} \tan t = \frac{\sin t}{\cos t} \\ \sec t = \frac{1}{\cos t} \\ \csc t = \frac{1}{\sin t} \\ c o t t = \frac{1}{tan t} = \frac{cos t}{sin t} \end{array}$
Sum and Difference Identities	$\begin{array}{l} \cos (α + β) = \cos α \cos β - \sin α \sin β \\ \cos (α - β) = \cos α \cos β + \sin α \sin β \\ \sin (α + β) = \sin α \cos β + \cos α \sin β \\ \sin (α - β) = \sin α \cos β - \cos α \sin β \\ \tan (α + β) = \frac{\tan α + \tan β}{1 - \tan α \tan β} \\ \tan (α - β) = \frac{\tan α - \tan β}{1 + \tan α \tan β} \end{array}$
Double-Angle Formulas	$\begin{array}{l} \sin (2 θ) = 2 \sin θ \cos θ \\ \cos (2 θ) = \cos^{2} θ - \sin^{2} θ \\ \cos (2 θ) = 1 - 2 \sin^{2} θ \\ \cos (2 θ) = 2 \cos^{2} θ - 1 \\ \tan (2 θ) = \frac{2 \tan θ}{1 - \tan^{2} θ} \end{array}$
Half-Angle Formulas	$\begin{array}{l} \sin \frac{α}{2} = \pm \sqrt{\frac{1 - \cos α}{2}} \\ \cos \frac{α}{2} = \pm \sqrt{\frac{1 + \cos α}{2}} \\ \tan \frac{α}{2} = \pm \sqrt{\frac{1 - \cos α}{1 + \cos α}} \\ \tan \frac{α}{2} = \frac{\sin α}{1 + \cos α} \\ \tan \frac{α}{2} = \frac{1 - \cos α}{\sin α} \end{array}$
Reduction Formulas	$\begin{array}{l} \sin^{2} θ = \frac{1 - \cos (2 θ)}{2} \\ \cos^{2} θ = \frac{1 + \cos (2 θ)}{2} \\ \tan^{2} θ = \frac{1 - \cos (2 θ)}{1 + \cos (2 θ)} \end{array}$
Product-to-Sum Formulas	$\begin{array}{l} \cos α \cos β = \frac{1}{2} [\cos (α - β) + \cos (α + β)] \\ \sin α \cos β = \frac{1}{2} [\sin (α + β) + \sin (α - β)] \\ \sin α \sin β = \frac{1}{2} [\cos (α - β) - \cos (α + β)] \\ \cos α \sin β = \frac{1}{2} [\sin (α + β) - \sin (α - β)] \end{array}$
Sum-to-Product Formulas	$\begin{array}{l} \sin α + \sin β = 2 \sin (\frac{α + β}{2}) \cos (\frac{α - β}{2}) \\ \sin α - \sin β = 2 \sin (\frac{α - β}{2}) \cos (\frac{α + β}{2}) \\ \cos α - \cos β = - 2 \sin (\frac{α + β}{2}) \sin (\frac{α - β}{2}) \\ \cos α + \cos β = 2 \cos (\frac{α + β}{2}) \cos (\frac{α - β}{2}) \end{array}$
Law of Sines	$\begin{array}{l} \frac{\sin α}{a} = \frac{\sin β}{b} = \frac{\sin γ}{c} \\ \frac{a}{\sin α} = \frac{b}{\sin β} = \frac{c}{\sin γ} \end{array}$
Law of Cosines	$\begin{matrix} a^{2} = b^{2} + c^{2} - 2 b c \cos α \\ b^{2} = a^{2} + c^{2} - 2 a c \cos β \\ c^{2} = a^{2} + b^{2} - 2 a b cos γ \end{matrix}$

Toolkit functions

Three graphs side-by-side. From left to right, graph of the identify function, square function, and square root function. All three graphs extend from -4 to 4 on each axis.

Three graphs side-by-side. From left to right, graph of the cubic function, cube root function, and reciprocal function. All three graphs extend from -4 to 4 on each axis.

Three graphs side-by-side. From left to right, graph of the absolute value function, exponential function, and natural logarithm function. All three graphs extend from -4 to 4 on each axis.

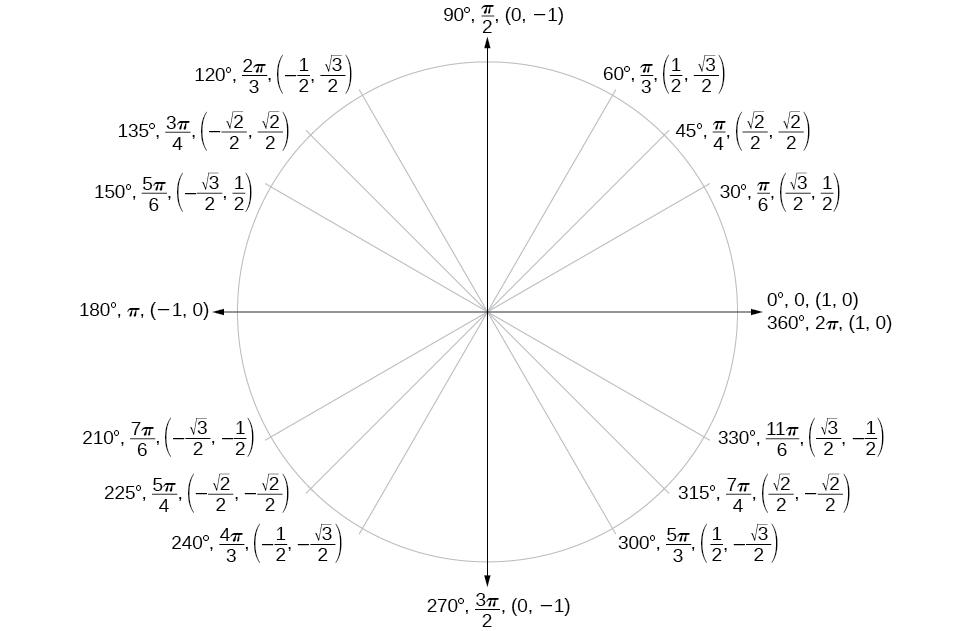
Trigonometric functions

Unit Circle

Angle	$0$	$\frac{π}{6}, or 30 °$	$\frac{π}{4}, or 45 °$	$\frac{π}{3}, or 60 °$	$\frac{π}{2}, or 90 °$
Cosine	1	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	0
Sine	0	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	1
Tangent	0	$\frac{\sqrt{3}}{3}$	1	$\sqrt{3}$	Undefined
Secant	1	$\frac{2 \sqrt{3}}{3}$	$\sqrt{2}$	2	Undefined
Cosecant	Undefined	2	$\sqrt{2}$	$\frac{2 \sqrt{3}}{3}$	1
Cotangent	Undefined	$\sqrt{3}$	1	$\frac{\sqrt{3}}{3}$	0

Questions & Answers

summarize halerambos & holbon

David Reply

the Three stages of Auguste Comte

Clementina Reply

what are agents of socialization

Antonio Reply

sociology of education

Nuhu Reply

definition of sociology of education

Nuhu

what is culture

Abdulrahim Reply

shared beliefs, values, and practices

AI-Robot

What are the two type of scientific method

ogunniran Reply

I'm willing to join you

Aceng Reply

what are the scientific method of sociology

Man

what is socialization

ogunniran Reply

the process wherein people come to understand societal norms and expectations, to accept society's beliefs, and to be aware of societal values

AI-Robot

scientific method in doing research

ogunniran

defimition of sickness in afica

Anita

Cosmology

ogunniran

Hmmm

ogunniran

list and explain the terms that found in society

REMMY Reply

list and explain the terms that found in society

Mukhtar

what are the agents of socialization

Antonio

Family Peer group Institution

Abdulwajud

I mean the definition

Antonio

ways of perceived deviance indifferent society

Naomi Reply

reasons of joining groups

SAM

to bring development to the nation at large

Hyellafiya

entails of consultative and consensus building from others

Gadama

World first Sociologist?

Abu

What is evolutionary model

Muhammad Reply

Evolution models refer to mathematical and computational representations of the processes involved in biological evolution. These models aim to simulate and understand how species change over time through mechanisms such as natural selection, genetic drift, and mutation. Evolutionary models can be u

faruk

what are the modern trends in religious behaviours

Selekeye Reply

what are social norms

Daniel Reply

shared standards of acceptable behavior by the group or appropriate behavior in a particular institution or those behaviors that are acceptable in a society

Lucius

that is how i understood it

Lucius

examples of societal norms

Diamond

Discuss the characteristics of the research located within positivist and the interpretivist paradigm

Tariro Reply

what is Industrialisation

Selekeye Reply

industrialization

Angelo

Got questions? Join the online conversation and get instant answers!

Jobilize.com Reply

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Algebra and trigonometry. OpenStax CNX. Nov 14, 2016 Download for free at https://legacy.cnx.org/content/col11758/1.6

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?

Ask

	4 Toolkit functions By OpenStax Read Online Course
	6 AP Key Terms 06 The Skeletal System By OpenStax Start Key Terms
	6 Enterprise JavaBeans By JavaChamp Team Start Quiz
	1 Sociology 01 An Introduction to Sociology MCQ By OpenStax Start Quiz
	9 Neuroanatomy 09 The Auditory System By Stephen Voron Start Quiz
	7 Sociology 07 Deviance, Crime, Social Control MCQ By OpenStax Start Quiz
	2 Biology 02 The Chemical Foundation of Life MCQ By OpenStax Start Quiz
	2 Sociology 02 Sociological Research MCQ By OpenStax Start Quiz
	4 Pharmacology Essay Excl. Nervous System By Rohini Ajay Start Test
	3 Sociology 03 Culture MCQ By OpenStax Start Quiz
	2 Psychology MCQ 2009 1 Exam By John Gabrieli Start Exam