10.5 Polar form of complex numbers  (Page 2/8)

Writing complex numbers in polar form

The polar form of a complex number    expresses a number in terms of an angle $\theta$ and its distance from the origin $r.$ Given a complex number in rectangular form expressed as $z=x+yi,$ we use the same conversion formulas as we do to write the number in trigonometric form:

We review these relationships in [link] .

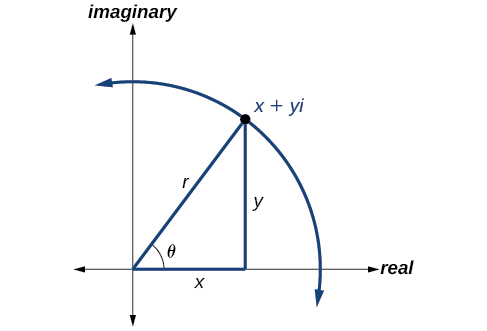
We use the term modulus to represent the absolute value of a complex number, or the distance from the origin to the point $\left(x,y\right).$ The modulus, then, is the same as $r,$ the radius in polar form. We use $\theta$ to indicate the angle of direction (just as with polar coordinates). Substituting, we have

Expressing a complex number using polar coordinates

Express the complex number $4i$ using polar coordinates.

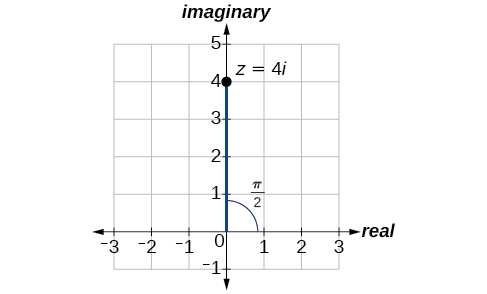
On the complex plane, the number $z=4i$ is the same as $z=0+4i.$ Writing it in polar form, we have to calculate $r$ first.

$$\begin{array}{l}r=\sqrt{x^2+y^2}\hfill \\ r=\sqrt{0^2+4^2}\hfill \\ r=\sqrt{16}\hfill \\ r=4\hfill \end{array}$$

Next, we look at $x.$ If $x=r\cos \theta ,$ and $x=0,$ then $\theta =\frac{\pi }{2}.$ In polar coordinates, the complex number $z=0+4i$ can be written as $z=4\left(\cos \left(\frac{\pi }{2}\right)+i\sin \left(\frac{\pi }{2}\right)\right)$ or $4\text{cis}\left(\frac{\pi }{2}\right).$ See [link] .

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Converting a complex number from polar to rectangular form

Converting a complex number from polar form to rectangular form is a matter of evaluating what is given and using the distributive property. In other words, given $z=r\left(\cos \theta +i\sin \theta \right),$ first evaluate the trigonometric functions $\cos \theta$ and $\sin \theta .$ Then, multiply through by $r.$

Finding products of complex numbers in polar form

Now that we can convert complex numbers to polar form we will learn how to perform operations on complex numbers in polar form. For the rest of this section, we will work with formulas developed by French mathematician Abraham de Moivre (1667-1754). These formulas have made working with products, quotients, powers, and roots of complex numbers much simpler than they appear. The rules are based on multiplying the moduli and adding the arguments.