7.6 Modeling with trigonometric equations (Page 3/14)

Precalculus

Page 3 / 14

Describing periodic motion

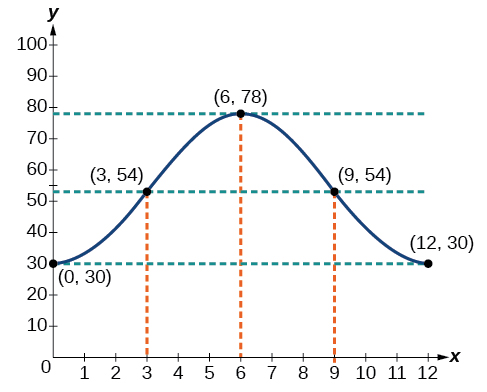
The hour hand of the large clock on the wall in Union Station measures 24 inches in length. At noon, the tip of the hour hand is 30 inches from the ceiling. At 3 PM, the tip is 54 inches from the ceiling, and at 6 PM, 78 inches. At 9 PM, it is again 54 inches from the ceiling, and at midnight, the tip of the hour hand returns to its original position 30 inches from the ceiling. Let $y$ equal the distance from the tip of the hour hand to the ceiling $x$ hours after noon. Find the equation that models the motion of the clock and sketch the graph.

Begin by making a table of values as shown in [link] .

$x$	$y$	Points to plot
Noon	30 in	$(0, 30)$
3 PM	54 in	$(3, 54)$
6 PM	78 in	$(6, 78)$
9 PM	54 in	$(9, 54)$
Midnight	30 in	$(12, 30)$

To model an equation, we first need to find the amplitude.

\begin{array}{l} \begin{array}{l} | A | = | \frac{78 - 30}{2} | \\ = 24 \end{array} \end{array}

The clock’s cycle repeats every 12 hours. Thus,

\begin{array}{l} \begin{array}{l} B = \frac{2 π}{12} \\ = \frac{π}{6} \end{array} \end{array}

The vertical shift is

\begin{array}{l} \begin{array}{l} D = \frac{78 + 30}{2} \\ = 54 \end{array} \end{array}

There is no horizontal shift, so $C = 0.$ Since the function begins with the minimum value of $y$ when $x = 0$ (as opposed to the maximum value), we will use the cosine function with the negative value for $A .$ In the form $y = A \cos (B x \pm C) + D,$ the equation is

y = −24 \cos (\frac{π}{6} x) + 54

See [link] .

Graph of the function y=-24cos(pi/6 x)+54 using the five key points: (0,30), (3,54), (6,78), (9,54), (12,30).

Got questions? Get instant answers now!

Determining a model for tides

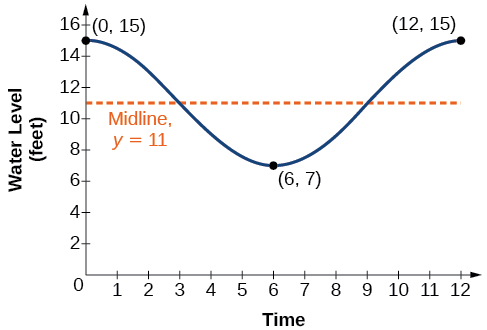
The height of the tide in a small beach town is measured along a seawall. Water levels oscillate between 7 feet at low tide and 15 feet at high tide. On a particular day, low tide occurred at 6 AM and high tide occurred at noon. Approximately every 12 hours, the cycle repeats. Find an equation to model the water levels.

As the water level varies from 7 ft to 15 ft, we can calculate the amplitude as

\begin{array}{l} \begin{array}{l} | A | = | \frac{(15 - 7)}{2} | \\ = 4 \end{array} \end{array}

The cycle repeats every 12 hours; therefore, $B$ is

\frac{2 π}{12} = \frac{π}{6}

There is a vertical translation of $\frac{(15 + 8)}{2} = 11.5.$ Since the value of the function is at a maximum at $t = 0,$ we will use the cosine function, with the positive value for $A .$

y = 4 \cos (\frac{π}{6}) t + 11

See [link] .

Graph of the function y=4cos(pi/6 t) + 11 from 0 to 12. The midline is y=11, three key points are (0,15), (6,7), and (12, 15).

Got questions? Get instant answers now!

Try It

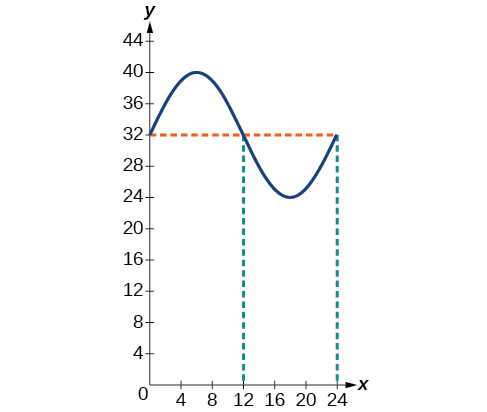
The daily temperature in the month of March in a certain city varies from a low of $24 °F$ to a high of $40 °F .$ Find a sinusoidal function to model daily temperature and sketch the graph. Approximate the time when the temperature reaches the freezing point $32 °F .$ Let $t = 0$ correspond to noon.

$y = 8 \sin (\frac{π}{12} t) + 32$
The temperature reaches freezing at noon and at midnight.

Graph of the function y=8sin(pi/12 t) + 32 for temperature. The midline is at 32. The times when the temperature is at 32 are midnight and noon.

Got questions? Get instant answers now!

Interpreting the periodic behavior equation

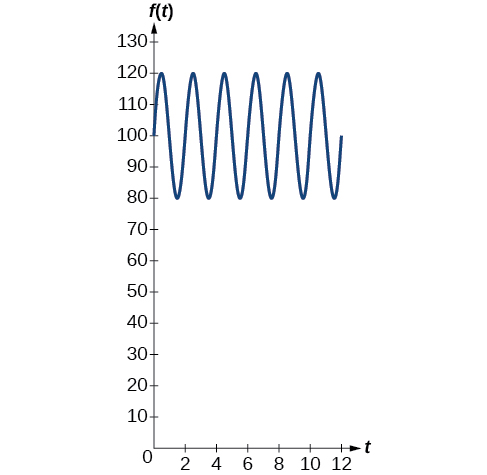
The average person’s blood pressure is modeled by the function $f (t) = 20 \sin (160 π t) + 100,$ where $f (t)$ represents the blood pressure at time $t,$ measured in minutes. Interpret the function in terms of period and frequency. Sketch the graph and find the blood pressure reading.

The period is given by

\begin{array}{l} \begin{array}{l} \frac{2 π}{ω} = \frac{2 π}{160 π} \\ = \frac{1}{80} \end{array} \end{array}

In a blood pressure function, frequency represents the number of heart beats per minute. Frequency is the reciprocal of period and is given by

\begin{matrix} \frac{ω}{2 π} = \frac{160 π}{2 π} \\ = 80 \end{matrix}

See the graph in [link] .

Graph of the function f(t) = 20sin(160 * pi * t) + 100 for blood pressure. The midline is at 100. — The blood pressure reading on the graph is $\frac{120}{80} (\frac{maximum}{minimum}) .$

Got questions? Get instant answers now!

Modeling harmonic motion functions

Harmonic motion is a form of periodic motion, but there are factors to consider that differentiate the two types. While general periodic motion applications cycle through their periods with no outside interference, harmonic motion requires a restoring force. Examples of harmonic motion include springs, gravitational force, and magnetic force.

Questions & Answers

Why is b in the answer

Dahsolar Reply

how do you work it out?

Brad Reply

answer

Ernest

heheheehe

Nitin

(Pcos∅+qsin∅)/(pcos∅-psin∅)

John Reply

how to do that?

Rosemary Reply

what is it about?

Amoah

how to answer the activity

Chabelita Reply

how to solve the activity

Chabelita

solve for X,,4^X-6(2^)-16=0

Alieu Reply

x4xminus 2

Lominate

sobhan Singh jina uniwarcity tignomatry ka long answers tile questions

harish Reply

t he silly nut company makes two mixtures of nuts: mixture a and mixture b. a pound of mixture a contains 12 oz of peanuts, 3 oz of almonds and 1 oz of cashews and sells for $4. a pound of mixture b contains 12 oz of peanuts, 2 oz of almonds and 2 oz of cashews and sells for $5. the company has 1080

ZAHRO Reply

If  , , are the roots of the equation 3 2 0, x px qx r     Find the value of 1  .

Swetha Reply

Parts of a pole were painted red, blue and yellow. 3/5 of the pole was red and 7/8 was painted blue. What part was painted yellow?

Patrick Reply

Parts of the pole was painted red, blue and yellow. 3 /5 of the pole was red and 7 /8 was painted blue. What part was painted yellow?

Patrick

how I can simplify algebraic expressions

Katleho Reply

Lairene and Mae are joking that their combined ages equal Sam’s age. If Lairene is twice Mae’s age and Sam is 69 yrs old, what are Lairene’s and Mae’s ages?

Mary Reply

23yrs

Yeboah

lairenea's age is 23yrs

ACKA

Katleho

Ello everyone

Katleho

Laurene is 46 yrs and Mae is 23 is

Solomon

hey people

christopher

age does not matter

christopher

solve for X, 4^x-6(2*)-16=0

Alieu

prove`x^3-3x-2cosA=0 (-π<A<=π

Mayank Reply

create a lesson plan about this lesson

Rose Reply

Excusme but what are you wrot?

Got questions? Join the online conversation and get instant answers!

Jobilize.com Reply

<< Chapter < Page Page > Chapter >>

Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Precalculus. OpenStax CNX. Jan 19, 2016 Download for free at https://legacy.cnx.org/content/col11667/1.6

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Precalculus' conversation and receive update notifications?

Ask

	5 Simple harmonic motion By OpenStax Read Online Course
	3 Modeling periodic behavior By OpenStax Read Online Course
	Financial Markets By Keyaira Braxton Start Exam
	13 AP 13 Nervous System Essay By OpenStax Start Flashcards
	10 Lec:10 Sampling Confidence Intervals By Janet Forrester Start Quiz
	Principles of macroeconomics for ap® courses By OpenStax Read Online Course
	Interviewing Skills MCQ By Mary Matera Start Quiz
	1 Biology 01 The Study of Life MCQ By OpenStax Start Quiz
	NCE Ch 06 Groups By Anh Dao Start Quiz
	24 AP 24 Metabolism Nutrition Essay By OpenStax Start Flashcards
	22 Biology 22 Prokaryotes Bacteria and Archaea MCQ By OpenStax Start Quiz
	Theater History Final - Review By Cameron Casey Start Exam