8.3 Polar coordinates

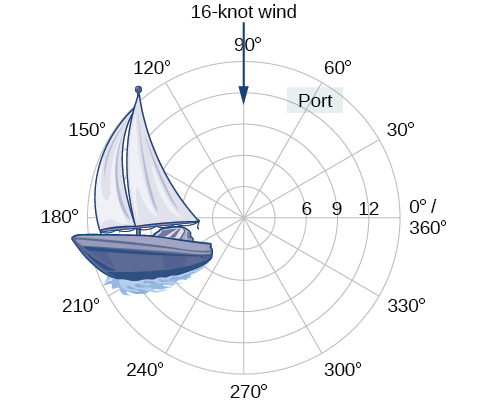
Over 12 kilometers from port, a sailboat encounters rough weather and is blown off course by a 16-knot wind (see [link] ). How can the sailor indicate his location to the Coast Guard? In this section, we will investigate a method of representing location that is different from a standard coordinate grid.

Plotting points using polar coordinates

When we think about plotting points in the plane, we usually think of rectangular coordinates $\left(x,y\right)$ in the Cartesian coordinate plane. However, there are other ways of writing a coordinate pair and other types of grid systems. In this section, we introduce to polar coordinates    , which are points labeled $\left(r,\theta \right)$ and plotted on a polar grid. The polar grid is represented as a series of concentric circles radiating out from the pole    , or the origin of the coordinate plane.

The polar grid is scaled as the unit circle with the positive x- axis now viewed as the polar axis    and the origin as the pole. The first coordinate $r$ is the radius or length of the directed line segment from the pole. The angle $\theta ,$ measured in radians, indicates the direction of $r.$ We move counterclockwise from the polar axis by an angle of $\theta ,$ and measure a directed line segment the length of $r$ in the direction of $\theta .$ Even though we measure $\theta$ first and then $r,$ the polar point is written with the r -coordinate first. For example, to plot the point $\left(2,\frac{\pi }{4}\right),$ we would move $\frac{\pi }{4}$ units in the counterclockwise direction and then a length of 2 from the pole. This point is plotted on the grid in [link] .

Plotting a point on the polar grid

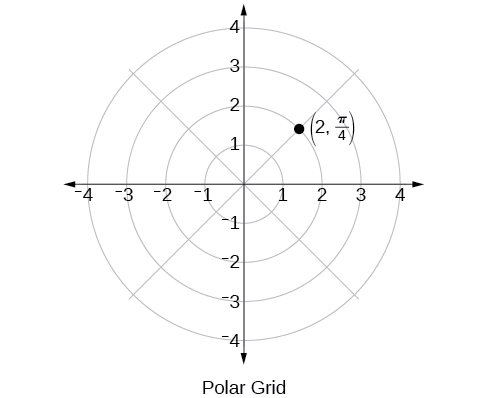
Plot the point $\left(3,\frac{\pi }{2}\right)$ on the polar grid.

The angle $\frac{\pi }{2}$ is found by sweeping in a counterclockwise direction 90° from the polar axis. The point is located at a length of 3 units from the pole in the $\frac{\pi }{2}$ direction, as shown in [link] .

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Plotting a point in the polar coordinate system with a negative component

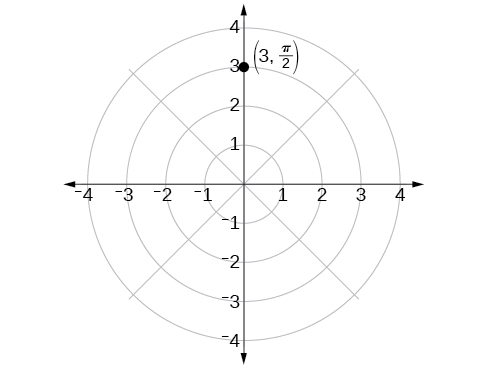
Plot the point $\left(-2,\frac{\pi }{6}\right)$ on the polar grid.

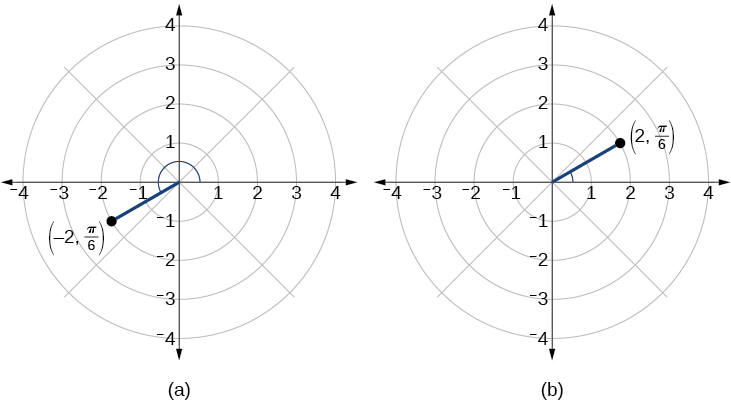
We know that $\frac{\pi }{6}$ is located in the first quadrant. However, $r=\mathrm{-2.}$ We can approach plotting a point with a negative $r$ in two ways:

1. Plot the point $\left(2,\frac{\pi }{6}\right)$ by moving $\frac{\pi }{6}$ in the counterclockwise direction and extending a directed line segment 2 units into the first quadrant. Then retrace the directed line segment back through the pole, and continue 2 units into the third quadrant;
2. Move $\frac{\pi }{6}$ in the counterclockwise direction, and draw the directed line segment from the pole 2 units in the negative direction, into the third quadrant.

See [link] (a). Compare this to the graph of the polar coordinate $\left(2,\frac{\pi }{6}\right)$ shown in [link] (b).

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Try It

Plot the points $\left(3,-\frac{\pi }{6}\right)$ and $\left(2,\frac{9\pi }{4}\right)$ on the same polar grid.

Got questions? Get instant answers now!

Converting from polar coordinates to rectangular coordinates

When given a set of polar coordinates    , we may need to convert them to rectangular coordinates . To do so, we can recall the relationships that exist among the variables $x,y,r,$ and $\theta .$