| << Chapter < Page | Chapter >> Page > |
The vector component form of the displacement vector is
This solution is shown in [link] .
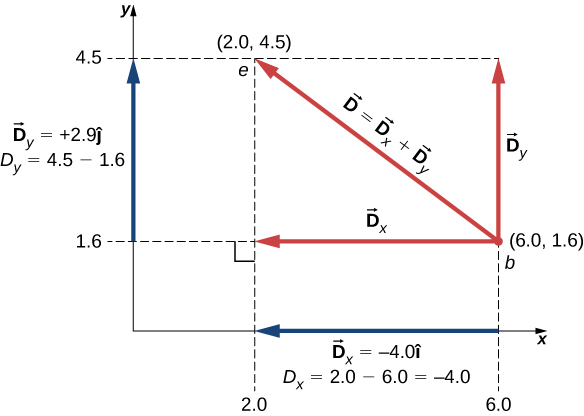
The vector x -component of the displacement vector has the magnitude because the magnitude of the unit vector is . Notice, too, that the direction of the x -component is , which is antiparallel to the direction of the + x -axis; hence, the x -component vector points to the left, as shown in [link] . The scalar x -component of vector is .
Similarly, the vector y -component of the displacement vector has magnitude because the magnitude of the unit vector is . The direction of the y -component is , which is parallel to the direction of the + y -axis. Therefore, the y -component vector points up, as seen in [link] . The scalar y -component of vector is . The displacement vector is the resultant of its two vector components.
The vector component form of the displacement vector [link] tells us that the mouse pointer has been moved on the monitor 4.0 cm to the left and 2.9 cm upward from its initial position.
Check Your Understanding A blue fly lands on a sheet of graph paper at a point located 10.0 cm to the right of its left edge and 8.0 cm above its bottom edge and walks slowly to a point located 5.0 cm from the left edge and 5.0 cm from the bottom edge. Choose the rectangular coordinate system with the origin at the lower left-side corner of the paper and find the displacement vector of the fly. Illustrate your solution by graphing.
; the fly moved 5.0 cm to the left and 3.0 cm down from its landing site.

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?