| << Chapter < Page | Chapter >> Page > |
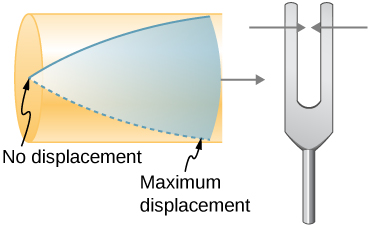
The standing wave formed in the tube has an antinode at the open end and a node at the closed end. The distance from a node to an antinode is one-fourth of a wavelength, and this equals the length of the tube; thus, This same resonance can be produced by a vibration introduced at or near the closed end of the tube ( [link] ). It is best to consider this a natural vibration of the air column, independently of how it is induced.
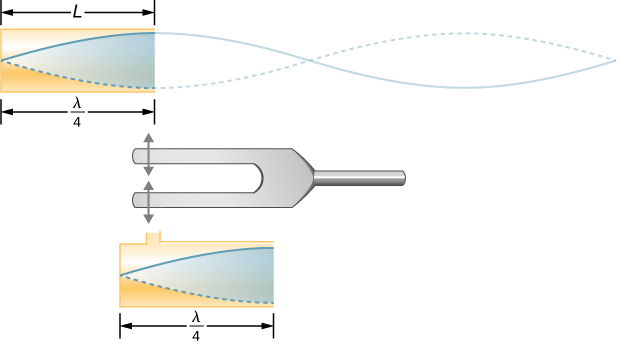
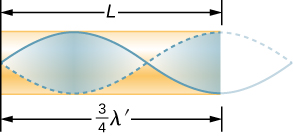
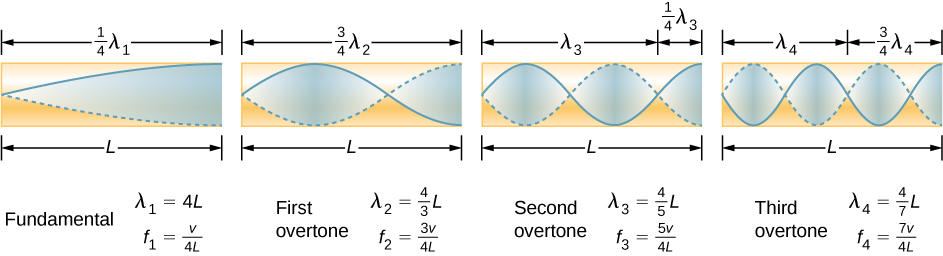
Given that maximum air displacements are possible at the open end and none at the closed end, other shorter wavelengths can resonate in the tube, such as the one shown in [link] . Here the standing wave has three-fourths of its wavelength in the tube, or so that Continuing this process reveals a whole series of shorter-wavelength and higher-frequency sounds that resonate in the tube. We use specific terms for the resonances in any system. The lowest resonant frequency is called the fundamental , while all higher resonant frequencies are called overtones . All resonant frequencies are integral multiples of the fundamental, and they are collectively called harmonics . The fundamental is the first harmonic, the first overtone is the second harmonic, and so on. [link] shows the fundamental and the first three overtones (the first four harmonics) in a tube closed at one end.
The relationship for the resonant wavelengths of a tube closed at one end is
Now let us look for a pattern in the resonant frequencies for a simple tube that is closed at one end. The fundamental has and frequency is related to wavelength and the speed of sound as given by
Solving for f in this equation gives
where v is the speed of sound in air. Similarly, the first overtone has (see [link] ), so that
Because we call the first overtone the third harmonic. Continuing this process, we see a pattern that can be generalized in a single expression. The resonant frequencies of a tube closed at one end are
where is the fundamental, is the first overtone, and so on. It is interesting that the resonant frequencies depend on the speed of sound and, hence, on temperature. This dependence poses a noticeable problem for organs in old unheated cathedrals, and it is also the reason why musicians commonly bring their wind instruments to room temperature before playing them.

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?