10.7 Gyroscopic effects: vector aspects of angular momentum  (Page 2/3)

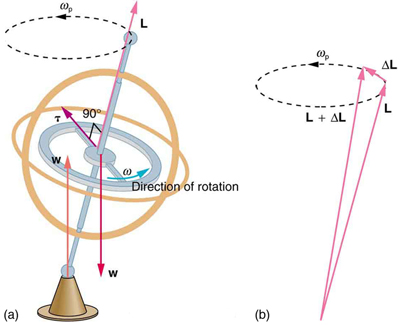
This same logic explains the behavior of gyroscopes. [link] shows the two forces acting on a spinning gyroscope. The torque produced is perpendicular to the angular momentum, thus the direction of the torque is changed, but not its magnitude. The gyroscope precesses around a vertical axis, since the torque is always horizontal and perpendicular to $\mathbf{\text{L}}$ . If the gyroscope is not spinning, it acquires angular momentum in the direction of the torque ( $\mathbf{\text{L}}=\text{Δ}\mathbf{\text{L}}$ ), and it rotates around a horizontal axis, falling over just as we would expect.

Earth itself acts like a gigantic gyroscope. Its angular momentum is along its axis and points at Polaris, the North Star. But Earth is slowly precessing (once in about 26,000 years) due to the torque of the Sun and the Moon on its nonspherical shape.

Section summary

• Torque is perpendicular to the plane formed by $r$ and $\mathbf{\text{F}}$ and is the direction your right thumb would point if you curled the fingers of your right hand in the direction of $\mathbf{\text{F}}$ . The direction of the torque is thus the same as that of the angular momentum it produces.
• The gyroscope precesses around a vertical axis, since the torque is always horizontal and perpendicular to $\mathbf{\text{L}}$ . If the gyroscope is not spinning, it acquires angular momentum in the direction of the torque ( $\mathbf{\text{L}}=\text{Δ}\mathbf{\text{L}}$ ), and it rotates about a horizontal axis, falling over just as we would expect.
• Earth itself acts like a gigantic gyroscope. Its angular momentum is along its axis and points at Polaris, the North Star.

Conceptual questions

Problem exercises

Integrated Concepts

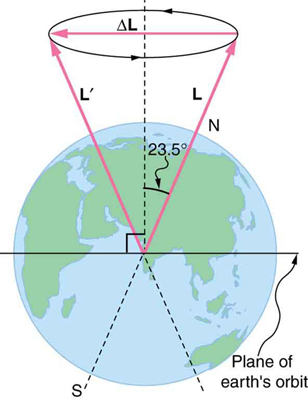
The axis of Earth makes a 23.5° angle with a direction perpendicular to the plane of Earth’s orbit. As shown in [link] , this axis precesses, making one complete rotation in 25,780 y.

(a) Calculate the change in angular momentum in half this time.

(b) What is the average torque producing this change in angular momentum?

(c) If this torque were created by a single force (it is not) acting at the most effective point on the equator, what would its magnitude be?

(a) $5\text{.}\text{64}\times {\text{10}}^{\text{33}}\text{kg}\cdot {\text{m}}^2\text{/s}$

(b) $1\text{.}\text{39}\times {\text{10}}^{\text{22}}\text{N}\cdot \text{m}$

(c) $2\text{.}\text{17}\times {\text{10}}^{\text{15}}\text{N}$

Got questions? Get instant answers now!