| << Chapter < Page | Chapter >> Page > |
In statics, the net torque is zero, and there is no angular acceleration. In rotational motion, net torque is the cause of angular acceleration, exactly as in Newton’s second law of motion for rotation.
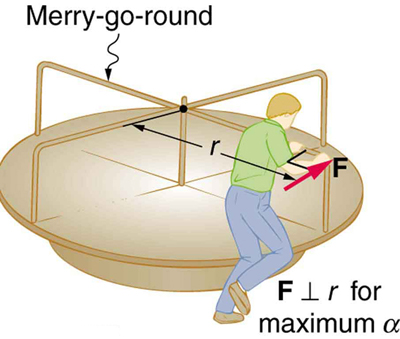
Consider the father pushing a playground merry-go-round in [link] . He exerts a force of 250 N at the edge of the 50.0-kg merry-go-round, which has a 1.50 m radius. Calculate the angular acceleration produced (a) when no one is on the merry-go-round and (b) when an 18.0-kg child sits 1.25 m away from the center. Consider the merry-go-round itself to be a uniform disk with negligible retarding friction.
Strategy
Angular acceleration is given directly by the expression :
To solve for , we must first calculate the torque (which is the same in both cases) and moment of inertia (which is greater in the second case). To find the torque, we note that the applied force is perpendicular to the radius and friction is negligible, so that
Solution for (a)
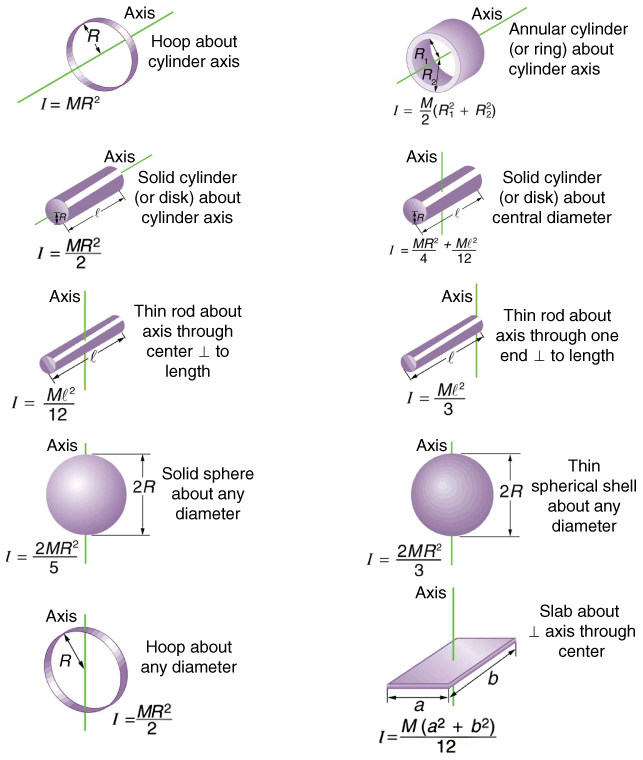
The moment of inertia of a solid disk about this axis is given in [link] to be
where and , so that
Now, after we substitute the known values, we find the angular acceleration to be
Solution for (b)
We expect the angular acceleration for the system to be less in this part, because the moment of inertia is greater when the child is on the merry-go-round. To find the total moment of inertia , we first find the child’s moment of inertia by considering the child to be equivalent to a point mass at a distance of 1.25 m from the axis. Then,
The total moment of inertia is the sum of moments of inertia of the merry-go-round and the child (about the same axis). To justify this sum to yourself, examine the definition of :
Substituting known values into the equation for gives
Discussion
The angular acceleration is less when the child is on the merry-go-round than when the merry-go-round is empty, as expected. The angular accelerations found are quite large, partly due to the fact that friction was considered to be negligible. If, for example, the father kept pushing perpendicularly for 2.00 s, he would give the merry-go-round an angular velocity of 13.3 rad/s when it is empty but only 8.89 rad/s when the child is on it. In terms of revolutions per second, these angular velocities are 2.12 rev/s and 1.41 rev/s, respectively. The father would end up running at about 50 km/h in the first case. Summer Olympics, here he comes! Confirmation of these numbers is left as an exercise for the reader.

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?