| << Chapter < Page | Chapter >> Page > |
Lenses are found in a huge array of optical instruments, ranging from a simple magnifying glass to the eye to a camera’s zoom lens. In this section, we will use the law of refraction to explore the properties of lenses and how they form images.
The word lens derives from the Latin word for a lentil bean, the shape of which is similar to the convex lens in [link] . The convex lens shown has been shaped so that all light rays that enter it parallel to its axis cross one another at a single point on the opposite side of the lens. (The axis is defined to be a line normal to the lens at its center, as shown in [link] .) Such a lens is called a converging (or convex) lens for the converging effect it has on light rays. An expanded view of the path of one ray through the lens is shown, to illustrate how the ray changes direction both as it enters and as it leaves the lens. Since the index of refraction of the lens is greater than that of air, the ray moves towards the perpendicular as it enters and away from the perpendicular as it leaves. (This is in accordance with the law of refraction.) Due to the lens’s shape, light is thus bent toward the axis at both surfaces. The point at which the rays cross is defined to be the focal point F of the lens. The distance from the center of the lens to its focal point is defined to be the focal length of the lens. [link] shows how a converging lens, such as that in a magnifying glass, can converge the nearly parallel light rays from the sun to a small spot.
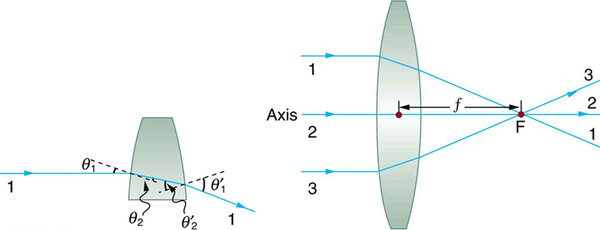
The lens in which light rays that enter it parallel to its axis cross one another at a single point on the opposite side with a converging effect is called converging lens.
The point at which the light rays cross is called the focal point F of the lens.
The distance from the center of the lens to its focal point is called focal length .

The greater effect a lens has on light rays, the more powerful it is said to be. For example, a powerful converging lens will focus parallel light rays closer to itself and will have a smaller focal length than a weak lens. The light will also focus into a smaller and more intense spot for a more powerful lens. The power of a lens is defined to be the inverse of its focal length. In equation form, this is

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?