| << Chapter < Page | Chapter >> Page > |
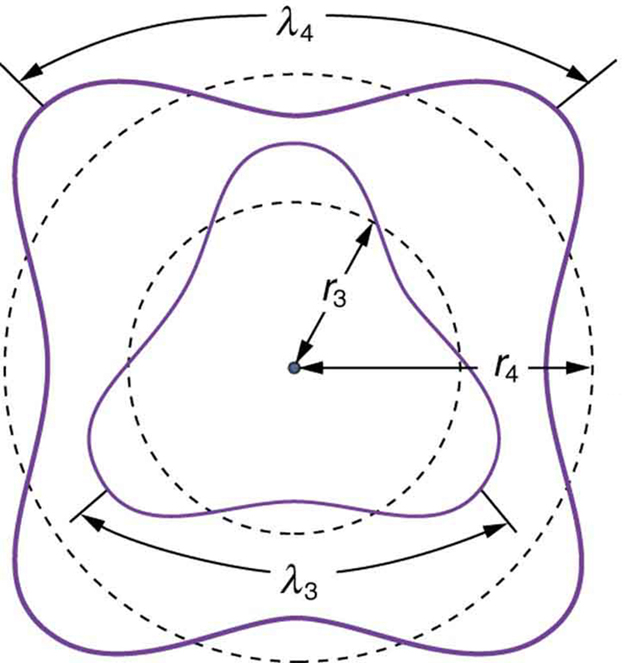
Rearranging terms, and noting that for a circular orbit, we obtain the quantization of angular momentum as the condition for allowed orbits:
This is what Bohr was forced to hypothesize as the rule for allowed orbits, as stated earlier. We now realize that it is the condition for constructive interference of an electron in a circular orbit. [link] illustrates this for and
The wave nature of matter is responsible for the quantization of energy levels in bound systems. Only those states where matter interferes constructively exist, or are “allowed.” Since there is a lowest orbit where this is possible in an atom, the electron cannot spiral into the nucleus. It cannot exist closer to or inside the nucleus. The wave nature of matter is what prevents matter from collapsing and gives atoms their sizes.
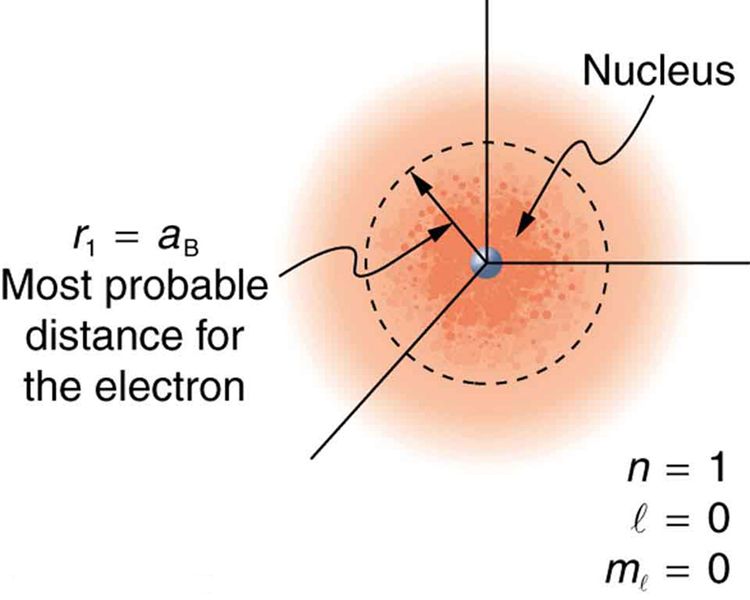
Because of the wave character of matter, the idea of well-defined orbits gives way to a model in which there is a cloud of probability, consistent with Heisenberg’s uncertainty principle. [link] shows how this applies to the ground state of hydrogen. If you try to follow the electron in some well-defined orbit using a probe that has a small enough wavelength to get some details, you will instead knock the electron out of its orbit. Each measurement of the electron’s position will find it to be in a definite location somewhere near the nucleus. Repeated measurements reveal a cloud of probability like that in the figure, with each speck the location determined by a single measurement. There is not a well-defined, circular-orbit type of distribution. Nature again proves to be different on a small scale than on a macroscopic scale.
There are many examples in which the wave nature of matter causes quantization in bound systems such as the atom. Whenever a particle is confined or bound to a small space, its allowed wavelengths are those which fit into that space. For example, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. This is true in blackbody radiators (atoms and molecules) as well as in atomic and molecular spectra. Various atoms and molecules will have different sets of electron orbits, depending on the size and complexity of the system. When a system is large, such as a grain of sand, the tiny particle waves in it can fit in so many ways that it becomes impossible to see that the allowed states are discrete. Thus the correspondence principle is satisfied. As systems become large, they gradually look less grainy, and quantization becomes less evident. Unbound systems (small or not), such as an electron freed from an atom, do not have quantized energies, since their wavelengths are not constrained to fit in a certain volume.
When do photons, electrons, and atoms behave like particles and when do they behave like waves? Watch waves spread out and interfere as they pass through a double slit, then get detected on a screen as tiny dots. Use quantum detectors to explore how measurements change the waves and the patterns they produce on the screen.

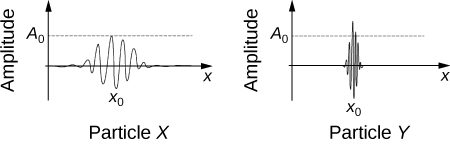
This figure shows graphical representations of the wave functions of two particles, X and Y , that are moving in the positive x -direction. The maximum amplitude of particle X ’s wave function is A 0 . Which particle has a greater probability of being located at position x 0 at this instant, and why?
(d)
In [link] , explain qualitatively the difference in the wave functions of particle X and particle Y . Which particle is more likely to be found at a larger distance from the coordinate x 0 and why? Which particle is more likely be found exactly at x 0 and why?
For an electron with a de Broglie wavelength , which of the following orbital circumferences within the atom would be disallowed? Select two answers.
(a), (c)
We have discovered that an electron’s orbit must contain an integer number of de Broglie wavelengths. Explain why, under ordinary conditions, this makes it impossible for electrons to spiral in to merge with the positively charged nucleus.
How is the de Broglie wavelength of electrons related to the quantization of their orbits in atoms and molecules?

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?