| << Chapter < Page | Chapter >> Page > |
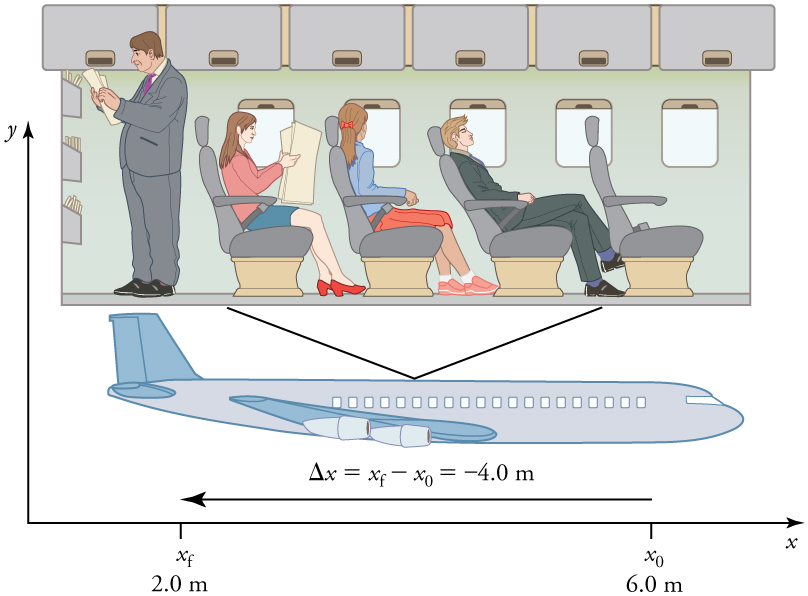
Note that displacement has a direction as well as a magnitude. The professor's displacement is 2.0 m to the right, and the airline passenger's displacement is 4.0 m toward the rear. In one-dimensional motion, direction can be specified with a plus or minus sign. When you begin a problem, you should select which direction is positive (usually that will be to the right or up, but you are free to select positive as being any direction). The professor's initial position is and her final position is . Thus her displacement is
In this coordinate system, motion to the right is positive, whereas motion to the left is negative. Similarly, the airplane passenger's initial position is and his final position is , so his displacement is
His displacement is negative because his motion is toward the rear of the plane, or in the negative direction in our coordinate system.
Although displacement is described in terms of direction, distance is not. Distance is defined to be the magnitude or size of displacement between two positions . Note that the distance between two positions is not the same as the distance traveled between them. Distance traveled is the total length of the path traveled between two positions . Distance has no direction and, thus, no sign. For example, the distance the professor walks is 2.0 m. The distance the airplane passenger walks is 4.0 m.
It is important to note that the distance traveled , however, can be greater than the magnitude of the displacement (by magnitude, we mean just the size of the displacement without regard to its direction; that is, just a number with a unit). For example, the professor could pace back and forth many times, perhaps walking a distance of 150 m during a lecture, yet still end up only 2.0 m to the right of her starting point. In this case her displacement would be +2.0 m, the magnitude of her displacement would be 2.0 m, but the distance she traveled would be 150 m. In kinematics we nearly always deal with displacement and magnitude of displacement, and almost never with distance traveled. One way to think about this is to assume you marked the start of the motion and the end of the motion. The displacement is simply the difference in the position of the two marks and is independent of the path taken in traveling between the two marks. The distance traveled, however, is the total length of the path taken between the two marks.
A cyclist rides 3 km west and then turns around and rides 2 km east. (a) What is her displacement? (b) What distance does she ride? (c) What is the magnitude of her displacement?
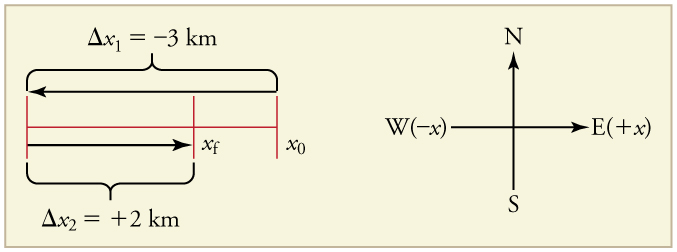
(a) The rider's displacement is . (The displacement is negative because we take east to be positive and west to be negative.)
(b) The distance traveled is .
(c) The magnitude of the displacement is .
Give an example in which there are clear distinctions among distance traveled, displacement, and magnitude of displacement. Specifically identify each quantity in your example.
Under what circumstances does distance traveled equal magnitude of displacement? What is the only case in which magnitude of displacement and displacement are exactly the same?
Bacteria move back and forth by using their flagella (structures that look like little tails). Speeds of up to have been observed. The total distance traveled by a bacterium is large for its size, while its displacement is small. Why is this?
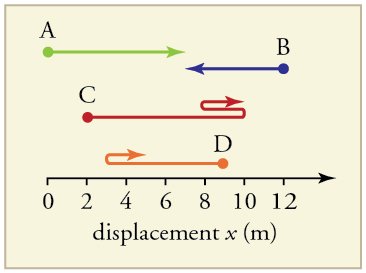
Find the following for path A in [link] : (a) The distance traveled. (b) The magnitude of the displacement from start to finish. (c) The displacement from start to finish.
(a) 7 m
(b) 7 m
(c)
Find the following for path B in [link] : (a) The distance traveled. (b) The magnitude of the displacement from start to finish. (c) The displacement from start to finish.
Find the following for path C in [link] : (a) The distance traveled. (b) The magnitude of the displacement from start to finish. (c) The displacement from start to finish.
(a) 13 m
(b) 9 m
(c)
Find the following for path D in [link] : (a) The distance traveled. (b) The magnitude of the displacement from start to finish. (c) The displacement from start to finish.
Which of the following statements comparing position, distance, and displacement is correct?
(b)

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?