| << Chapter < Page | Chapter >> Page > |
Now, we solve one of the rotational kinematics equations for . We start with the equation
Next, we solve for :
Substituting this into the equation for net and gathering terms yields
This equation is the work-energy theorem for rotational motion only. As you may recall, net work changes the kinetic energy of a system. Through an analogy with translational motion, we define the term to be rotational kinetic energy for an object with a moment of inertia and an angular velocity :
The expression for rotational kinetic energy is exactly analogous to translational kinetic energy, with being analogous to and to . Rotational kinetic energy has important effects. Flywheels, for example, can be used to store large amounts of rotational kinetic energy in a vehicle, as seen in [link] .
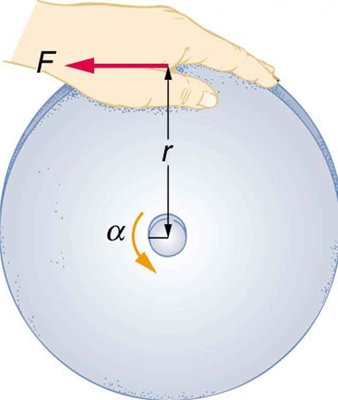
Consider a person who spins a large grindstone by placing her hand on its edge and exerting a force through part of a revolution as shown in [link] . In this example, we verify that the work done by the torque she exerts equals the change in rotational energy. (a) How much work is done if she exerts a force of 200 N through a rotation of ? The force is kept perpendicular to the grindstone's 0.320-m radius at the point of application, and the effects of friction are negligible. (b) What is the final angular velocity if the grindstone has a mass of 85.0 kg? (c) What is the final rotational kinetic energy? (It should equal the work.)
Strategy
To find the work, we can use the equation . We have enough information to calculate the torque and are given the rotation angle. In the second part, we can find the final angular velocity using one of the kinematic relationships. In the last part, we can calculate the rotational kinetic energy from its expression in .
Solution for (a)
The net work is expressed in the equation
where net is the applied force multiplied by the radius because there is no retarding friction, and the force is perpendicular to . The angle is given. Substituting the given values in the equation above yields
Noting that ,
Solution for (b)
To find from the given information requires more than one step. We start with the kinematic relationship in the equation
Note that because we start from rest. Taking the square root of the resulting equation gives

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?