6.7 Stokes’ theorem  (Page 4/10)

An amazing consequence of Stokes’ theorem is that if S ′ is any other smooth surface with boundary C and the same orientation as S , then ${\displaystyle {\iint }_S\text{curl}\text{F}·d\text{S}}={\displaystyle {\int }_C\text{F}·d\text{r}}=0$ because Stokes’ theorem says the surface integral depends on the line integral around the boundary only.

In [link] , we calculated a surface integral simply by using information about the boundary of the surface. In general, let $S_1$ and $S_2$ be smooth surfaces with the same boundary C and the same orientation. By Stokes’ theorem,

Therefore, if ${\displaystyle {\iint }_{S_1}\text{curl}\text{F}·d\text{S}}$ is difficult to calculate but ${\displaystyle {\iint }_{S_2}\text{curl}\text{F}·d\text{S}}$ is easy to calculate, Stokes’ theorem allows us to calculate the easier surface integral. In [link] , we could have calculated ${\displaystyle {\iint }_S\text{curl}\text{F}·d\text{S}}$ by calculating ${\displaystyle {\iint }_{S^{\prime }}\text{curl}\text{F}·d\text{S}},$ where $S^{\prime }$ is the disk enclosed by boundary curve C (a much more simple surface with which to work).

[link] shows that flux integrals of curl vector fields are surface independent    in the same way that line integrals of gradient fields are path independent. Recall that if F is a two-dimensional conservative vector field defined on a simply connected domain, $f$ is a potential function for F , and C is a curve in the domain of F , then ${\displaystyle {\int }_C\text{F}·d\text{r}}$ depends only on the endpoints of C . Therefore if C ′ is any other curve with the same starting point and endpoint as C (that is, C ′ has the same orientation as C ), then ${\displaystyle {\int }_C\text{F}·d\text{r}}={\displaystyle {\int }_{C\text{′}}\text{F}·d\text{r}}.$ In other words, the value of the integral depends on the boundary of the path only; it does not really depend on the path itself.

Analogously, suppose that S and S ′ are surfaces with the same boundary and same orientation, and suppose that G is a three-dimensional vector field that can be written as the curl of another vector field F (so that F is like a “potential field” of G ). By [link] ,

Therefore, the flux integral of G does not depend on the surface, only on the boundary of the surface. Flux integrals of vector fields that can be written as the curl of a vector field are surface independent in the same way that line integrals of vector fields that can be written as the gradient of a scalar function are path independent.

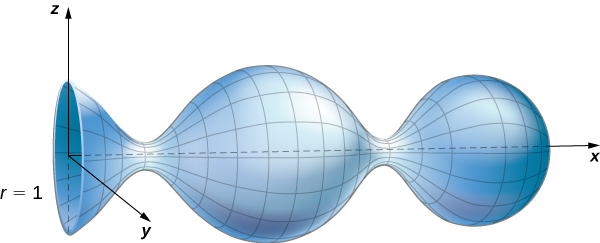
Use Stokes’ theorem to calculate surface integral ${\displaystyle {\iint }_S\text{curl}\text{F}·d\text{S}},$ where $\text{F}=⟨z,x,y⟩$ and S is the surface as shown in the following figure.

$\text{−}\pi$

Got questions? Get instant answers now!