4.7 Derivation of the fourier transform  (Page 3/3)

In communications, a very important operation on a signal $s(t)$ is to amplitude modulate it. Using this operation more as an example rather than elaborating the communicationsaspects here, we want to compute the Fourier transform — the spectrum — of $$(1+s(t))\cos (2\pi f_{c}t)$$ Thus, $$(1+s(t))\cos (2\pi f_{c}t)=\cos (2\pi f_{c}t)+s(t)\cos (2\pi f_{c}t)$$ For the spectrum of $\cos (2\pi f_{c}t)$ , we use the Fourier series. Its period is $\frac{1}{f_c}$ , and its only nonzero Fourier coefficients are $c_{\pm 1}=\frac{1}{2}$ . The second term is not periodic unless $s(t)$ has the same period as the sinusoid. Using Euler's relation, the spectrum of the second term can be derived as $$s(t)\cos (2\pi f_{c}t)=\int_{()} \,d f$$∞ ∞ S f 2 f t 2 f c t Using Euler's relation for the cosine, $$(s(t)\cos (2\pi f_{c}t))()=\frac{1}{2}\int_{()} \,d f$$∞ ∞ S f 2 f f c t 1 2 f ∞ ∞ S f 2 f f c t $$(s(t)\cos (2\pi f_{c}t))()=\frac{1}{2}\int_{()} \,d f$$∞ ∞ S f f c 2 f t 1 2 f ∞ ∞ S f f c 2 f t $$(s(t)\cos (2\pi f_{c}t))()=\int_{()} \,d f$$∞ ∞ S f f c S f f c 2 2 f t Exploiting the uniqueness property of the Fourier transform,we have

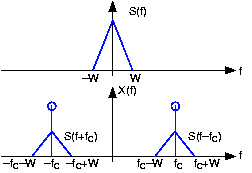
Note how in this figure the signal $s(t)$ is defined in the frequency domain. To find its time domain representation, we simply use the inverse Fourier transform.