3.4 Motion in space (Page 6/17)

Calculus volume 3 Page 6 / 17

T_{p}^{2} = D_{p}^{3}

for any planet in the solar system, where $T_{P}$ is the period of that planet measured in Earth years and $D_{P}$ is the average distance from that planet to the Sun measured in astronomical units. Therefore, if we know the average distance from a planet to the Sun (in astronomical units), we can then calculate the length of its year (in Earth years), and vice versa.

Kepler’s laws were formulated based on observations from Brahe; however, they were not proved formally until Sir Isaac Newton was able to apply calculus. Furthermore, Newton was able to generalize Kepler’s third law to other orbital systems, such as a moon orbiting around a planet. Kepler’s original third law only applies to objects orbiting the Sun.

Proof

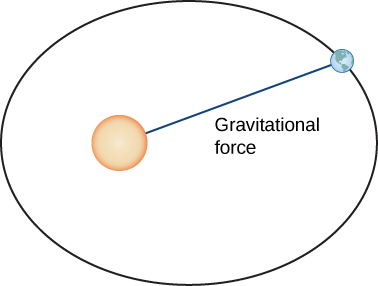
Let’s now prove Kepler’s first law using the calculus of vector-valued functions. First we need a coordinate system. Let’s place the Sun at the origin of the coordinate system and let the vector-valued function $r (t)$ represent the location of a planet as a function of time. Newton proved Kepler’s law using his second law of motion and his law of universal gravitation. Newton’s second law of motion can be written as $F = m a,$ where F represents the net force acting on the planet. His law of universal gravitation can be written in the form $F = - \frac{G m M}{{‖ r ‖}^{2}} \cdot \frac{r}{‖ r ‖},$ which indicates that the force resulting from the gravitational attraction of the Sun points back toward the Sun, and has magnitude $\frac{G m M}{{‖ r ‖}^{2}}$ ( [link] ).

This figure is an ellipse with a circle to the left on the inside at a focal point. The circle represents the sun. On the ellipse is a smaller circle representing Earth. The line segment drawn between the circles is labeled “gravitational force”. — The gravitational force between Earth and the Sun is equal to the mass of the earth times its acceleration.

Setting these two forces equal to each other, and using the fact that $a (t) = v^{'} (t),$ we obtain

m v^{'} (t) = - \frac{G m M}{{‖ r ‖}^{2}} \cdot \frac{r}{‖ r ‖},

which can be rewritten as

\frac{d v}{d t} = - \frac{G M}{{‖ r ‖}^{3}} r .

This equation shows that the vectors $d v / d t$ and r are parallel to each other, so $d v / d t \times r = 0 .$ Next, let’s differentiate $r \times v$ with respect to time:

\frac{d}{d t} (r \times v) = \frac{d r}{d t} \times v + r \times \frac{d v}{d t} = v \times v + 0 = 0 .

This proves that $r \times v$ is a constant vector, which we call C . Since $r$ and v are both perpendicular to C for all values of t , they must lie in a plane perpendicular to C . Therefore, the motion of the planet lies in a plane.

Next we calculate the expression $d v / d t \times C :$

\frac{d v}{d t} \times C = - \frac{G M}{{‖ r ‖}^{3}} r \times (r \times v) = - \frac{G M}{{‖ r ‖}^{3}} [(r \cdot v) r - (r \cdot r) v] .

The last equality in [link] is from the triple cross product formula ( Introduction to Vectors in Space ). We need an expression for $r \cdot v .$ To calculate this, we differentiate $r \cdot r$ with respect to time:

\frac{d}{d t} (r \cdot r) = \frac{d r}{d t} \cdot r + r \cdot \frac{d r}{d t} = 2 r \cdot \frac{d r}{d t} = 2 r \cdot v .

Since $r \cdot r = {‖ r ‖}^{2},$ we also have

\frac{d}{d t} (r \cdot r) = \frac{d}{d t} {‖ r ‖}^{2} = 2 ‖ r ‖ \frac{d}{d t} ‖ r ‖ .

Combining [link] and [link] , we get

\begin{matrix} 2 r \cdot v & = & 2 ‖ r ‖ \frac{d}{d t} ‖ r ‖ \\ r \cdot v & = & ‖ r ‖ \frac{d}{d t} ‖ r ‖ . \end{matrix}

Substituting this into [link] gives us

\begin{matrix} \frac{d v}{d t} \times C & = - \frac{G M}{{‖ r ‖}^{3}} [(r \cdot v) r - (r \cdot r) v] \\ = - \frac{G M}{{‖ r ‖}^{3}} [‖ r ‖ (\frac{d}{d t} ‖ r ‖) r - {‖ r ‖}^{2} v] \\ = − G M [\frac{1}{{‖ r ‖}^{2}} (\frac{d}{d t} ‖ r ‖) r - \frac{1}{‖ r ‖} v] \\ = G M [\frac{v}{‖ r ‖} - \frac{r}{{‖ r ‖}^{2}} (\frac{d}{d t} ‖ r ‖)] . \end{matrix}

However,

\begin{matrix} \frac{d}{d t} \frac{r}{‖ r ‖} & = \frac{\frac{d}{d t} (r) ‖ r ‖ - r \frac{d}{d t} ‖ r ‖}{{‖ r ‖}^{2}} \\ = \frac{\frac{d r}{d t}}{‖ r ‖} - \frac{r}{{‖ r ‖}^{2}} \frac{d}{d t} ‖ r ‖ \\ = \frac{v}{‖ r ‖} - \frac{r}{{‖ r ‖}^{2}} \frac{d}{d t} ‖ r ‖ . \end{matrix}

Therefore, [link] becomes

\frac{d v}{d t} \times C = G M (\frac{d}{d t} \frac{r}{‖ r ‖}) .

Since C is a constant vector, we can integrate both sides and obtain

v \times C = G M \frac{r}{‖ r ‖} + D,

where D is a constant vector. Our goal is to solve for $‖ r ‖ .$ Let’s start by calculating $r \cdot (v \times C) :$

r \cdot (v \times C) = r \cdot (G M \frac{r}{‖ r ‖} + D) = G M \frac{{‖ r ‖}^{2}}{‖ r ‖} + r \cdot D = G M ‖ r ‖ + r \cdot D .

However, $r \cdot (v \times C) = (r \times v) \cdot C,$ so

(r \times v) \cdot C = G M ‖ r ‖ + r \cdot D .

Since $r \times v = C,$ we have

{‖ C ‖}^{2} = G M ‖ r ‖ + r \cdot D .

Note that $r \cdot D = ‖ r ‖ ‖ D ‖ cos θ,$ where $θ$ is the angle between r and D. Therefore,

<< Chapter < Page Page > Chapter >>

Practice Key Terms 6

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Calculus volume 3. OpenStax CNX. Feb 05, 2016 Download for free at http://legacy.cnx.org/content/col11966/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?

Ask

	English Composition 2 Final Practice By Madison Christian Start Test
©flickr: U.S.	Molecular Cellular Biology By Ann Schlosser Start Quiz
	12 Biology 12 Mendel's Experiments Heredity MCQ By OpenStax Start Quiz
	2 AP 02 Chemical Level of Organization MCQ By OpenStax Start Quiz
©flickr:	Health Reviewer MCQ By Edgar Delgado Start Quiz
	10 Clin Sci I - GI Twedt quiz By Brooke Delaney Start Quiz
	26 Biology 26 Seed Plants MCQ By OpenStax Start Quiz
	Art Reviewer MCQ By Edgar Delgado Start Quiz
	14 Sociology 14 Marriage and Family MCQ By OpenStax Start Quiz
	Computer System Engineering By Robert Morris Start Exam