| << Chapter < Page | Chapter >> Page > |
[T] The “bumpy sphere” with an equation in spherical coordinates is with and where and are positive numbers and and are positive integers, may be used in applied mathematics to model tumor growth.
For the following exercises, determine whether the statement is true or false . Justify the answer with a proof or a counterexample.
For vectors and and any given scalar
The symmetric equation for the line of intersection between two planes and is given by
False
If then is perpendicular to
For the following exercises, use the given vectors to find the quantities.
For the following exercises, find the unit vectors.
Find the unit vector that has the same direction as vector that begins at and ends at
Find the unit vector that has the same direction as vector that begins at and ends at
For the following exercises, find the area or volume of the given shapes.
The parallelogram spanned by vectors
For the following exercises, find the vector and parametric equations of the line with the given properties.
The line that passes through point that is parallel to vector
For the following exercises, find the equation of the plane with the given properties.
The plane that passes through point and has normal vector
For the following exercises, find the traces for the surfaces in planes Then, describe and draw the surfaces.
trace:
is a circle,
trace:
is a hyperbola (or a pair of lines if
trace:
is a hyperbola (or a pair of lines if
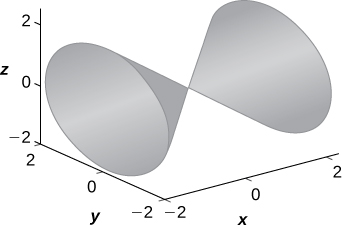
The surface is a cone.
For the following exercises, write the given equation in cylindrical coordinates and spherical coordinates.
For the following exercises, convert the given equations from cylindrical or spherical coordinates to rectangular coordinates. Identify the given surface.
For the following exercises, consider a small boat crossing a river.
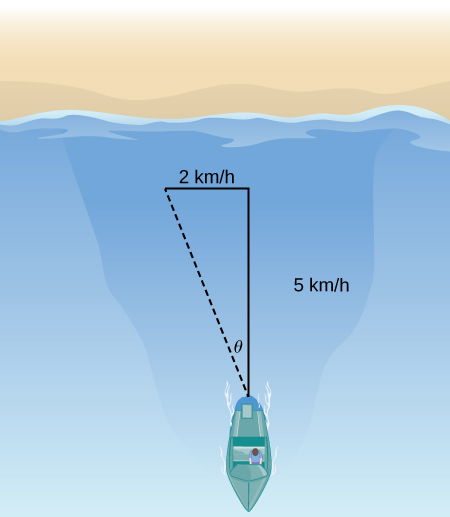
If the boat velocity is km/h due north in still water and the water has a current of km/h due west (see the following figure), what is the velocity of the boat relative to shore? What is the angle that the boat is actually traveling?
When the boat reaches the shore, two ropes are thrown to people to help pull the boat ashore. One rope is at an angle of and the other is at If the boat must be pulled straight and at a force of find the magnitude of force for each rope (see the following figure).
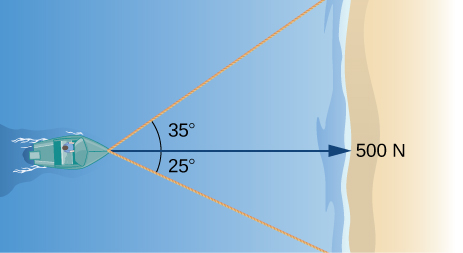
331 N, and 244 N
An airplane is flying in the direction of 52° east of north with a speed of 450 mph. A strong wind has a bearing 33° east of north with a speed of 50 mph. What is the resultant ground speed and bearing of the airplane?
Calculate the work done by moving a particle from position to along a straight line with a force
The following problems consider your unsuccessful attempt to take the tire off your car using a wrench to loosen the bolts. Assume the wrench is m long and you are able to apply a 200-N force.
Because your tire is flat, you are only able to apply your force at a angle. What is the torque at the center of the bolt? Assume this force is not enough to loosen the bolt.
Someone lends you a tire jack and you are now able to apply a 200-N force at an angle. Is your resulting torque going to be more or less? What is the new resulting torque at the center of the bolt? Assume this force is not enough to loosen the bolt.
More, J

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?