| << Chapter < Page | Chapter >> Page > |
Plot the point with spherical coordinates and describe its location in both rectangular and cylindrical coordinates.
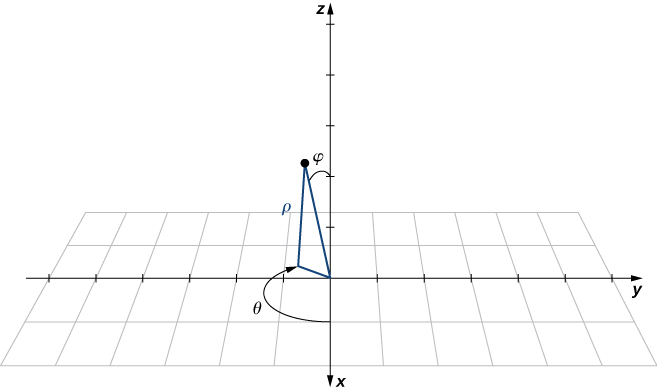
Cartesian:
cylindrical:
Convert the rectangular coordinates to both spherical and cylindrical coordinates.
Start by converting from rectangular to spherical coordinates:
Because then the correct choice for is
There are actually two ways to identify We can use the equation A more simple approach, however, is to use equation We know that and so
and therefore The spherical coordinates of the point are
To find the cylindrical coordinates for the point, we need only find
The cylindrical coordinates for the point are
Describe the surfaces with the given spherical equations.
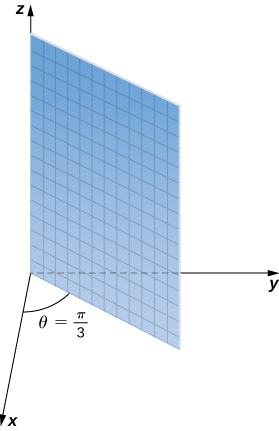
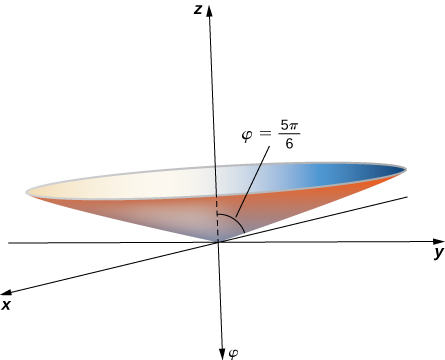
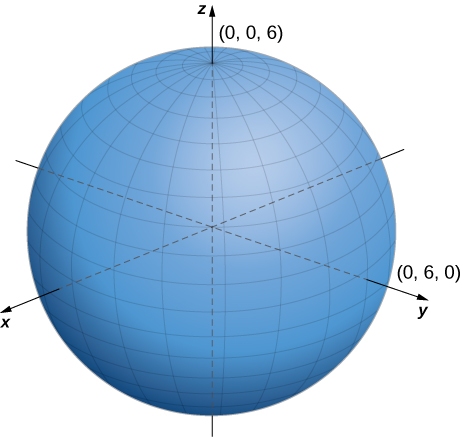
Describe the surfaces defined by the following equations.
a. This is the set of all points units from the origin. This set forms a sphere with radius b. This set of points forms a half plane. The angle between the half plane and the positive x -axis is c. Let be a point on this surface. The position vector of this point forms an angle of with the positive z -axis, which means that points closer to the origin are closer to the axis. These points form a half-cone.

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?