| << Chapter < Page | Chapter >> Page > |

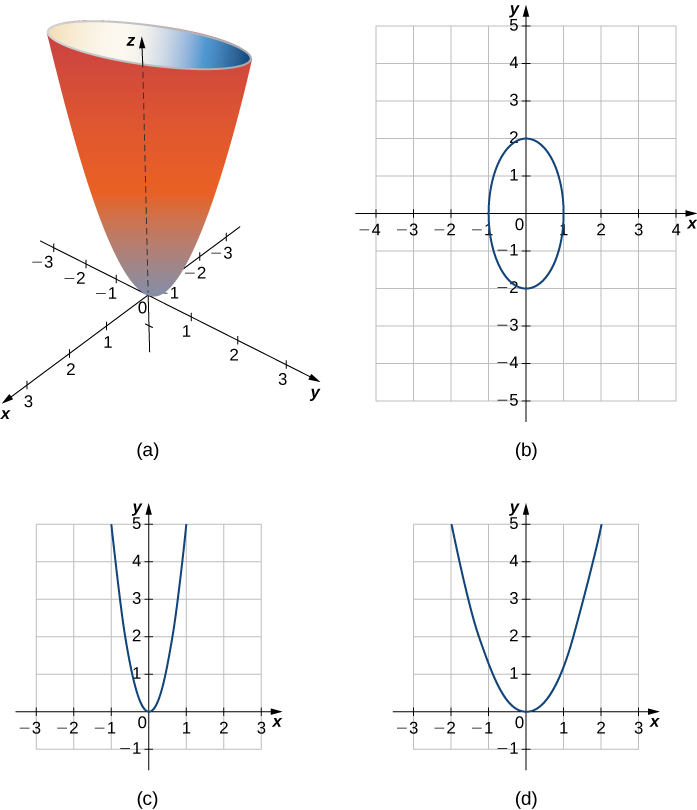
Describe the traces of the elliptic paraboloid
To find the trace in the xy -plane, set The trace in the plane is simply one point, the origin. Since a single point does not tell us what the shape is, we can move up the z -axis to an arbitrary plane to find the shape of other traces of the figure.
The trace in plane is the graph of equation which is an ellipse. In the xz -plane, the equation becomes The trace is a parabola in this plane and in any plane with the equation
In planes parallel to the yz -plane, the traces are also parabolas, as we can see in the following figure.
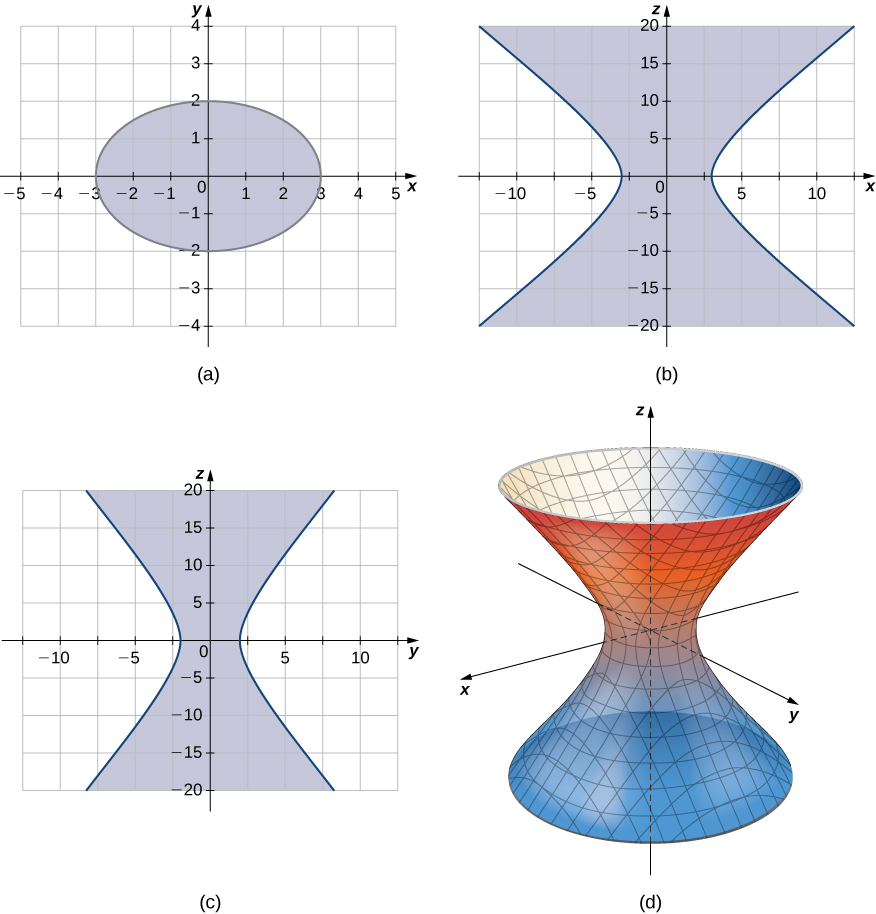
A hyperboloid of one sheet is any surface that can be described with an equation of the form Describe the traces of the hyperboloid of one sheet given by equation
The traces parallel to the
xy -plane are ellipses and the traces parallel to the
xz - and
yz -planes are hyperbolas. Specifically, the trace in the
xy -plane is ellipse
the trace in the
xz -plane is hyperbola
and the trace in the
yz -plane is hyperbola
(see the following figure).
Hyperboloids of one sheet have some fascinating properties. For example, they can be constructed using straight lines, such as in the sculpture in [link] (a). In fact, cooling towers for nuclear power plants are often constructed in the shape of a hyperboloid. The builders are able to use straight steel beams in the construction, which makes the towers very strong while using relatively little material ( [link] (b)).

Energy hitting the surface of a parabolic reflector is concentrated at the focal point of the reflector ( [link] ). If the surface of a parabolic reflector is described by equation where is the focal point of the reflector?
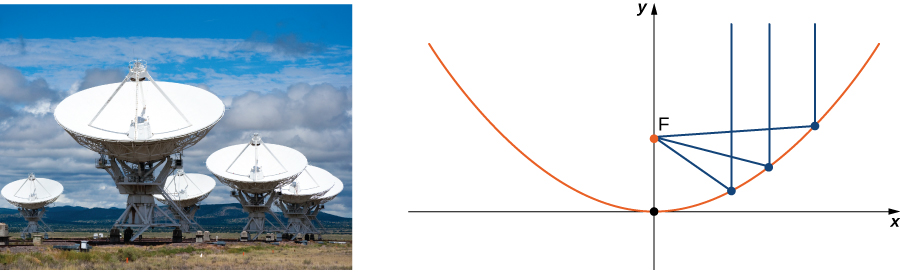
Since z is the first-power variable, the axis of the reflector corresponds to the z -axis. The coefficients of and are equal, so the cross-section of the paraboloid perpendicular to the z -axis is a circle. We can consider a trace in the xz -plane or the yz -plane; the result is the same. Setting the trace is a parabola opening up along the z -axis, with standard equation where is the focal length of the parabola. In this case, this equation becomes or So p is m, which tells us that the focus of the paraboloid is m up the axis from the vertex. Because the vertex of this surface is the origin, the focal point is
Seventeen standard quadric surfaces can be derived from the general equation

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?