2.4 The cross product (Page 4/16)

Page 4 / 16

Using expansion along the first row to compute a $3 \times 3$ Determinant

Evaluate the determinant $| \begin{matrix} 2 & 5 & −1 \\ −1 & 1 & 3 \\ −2 & 3 & 4 \end{matrix} | .$

We have

\begin{matrix} | \begin{matrix} 2 & 5 & −1 \\ −1 & 1 & 3 \\ −2 & 3 & 4 \end{matrix} | & = 2 | \begin{matrix} 1 & 3 \\ 3 & 4 \end{matrix} | - 5 | \begin{matrix} −1 & 3 \\ −2 & 4 \end{matrix} | - 1 | \begin{matrix} −1 & 1 \\ −2 & 3 \end{matrix} | \\ = 2 (4 - 9) - 5 (−4 + 6) - 1 (−3 + 2) \\ = 2 (−5) - 5 (2) - 1 (−1) = −10 - 10 + 1 \\ = −19. \end{matrix}

Got questions? Get instant answers now!

Evaluate the determinant $| \begin{matrix} 1 & −2 & −1 \\ 3 & 2 & −3 \\ 1 & 5 & 4 \end{matrix} | .$

$40$

Got questions? Get instant answers now!

Technically, determinants are defined only in terms of arrays of real numbers. However, the determinant notation provides a useful mnemonic device for the cross product formula.

Rule: cross product calculated by a determinant

Let $u = ⟨ u_{1}, u_{2}, u_{3} ⟩$ and $v = ⟨ v_{1}, v_{2}, v_{3} ⟩$ be vectors. Then the cross product $u \times v$ is given by

u \times v = | \begin{matrix} i & j & k \\ u_{1} & u_{2} & u_{3} \\ v_{1} & v_{2} & v_{3} \end{matrix} | = | \begin{matrix} u_{2} & u_{3} \\ v_{2} & v_{3} \end{matrix} | i - | \begin{matrix} u_{1} & u_{3} \\ v_{1} & v_{3} \end{matrix} | j + | \begin{matrix} u_{1} & u_{2} \\ v_{1} & v_{2} \end{matrix} | k .

Using determinant notation to find $p \times q$

Let $p = ⟨ −1, 2, 5 ⟩$ and $q = ⟨ 4, 0, −3 ⟩ .$ Find $p \times q .$

We set up our determinant by putting the standard unit vectors across the first row, the components of $u$ in the second row, and the components of $v$ in the third row. Then, we have

\begin{matrix} p \times q & = | \begin{matrix} i & j & k \\ −1 & 2 & 5 \\ 4 & 0 & −3 \end{matrix} | = | \begin{matrix} 2 & 5 \\ 0 & −3 \end{matrix} | i - | \begin{matrix} −1 & 5 \\ 4 & −3 \end{matrix} | j + | \begin{matrix} −1 & 2 \\ 4 & 0 \end{matrix} | k \\ = (−6 - 0) i - (3 - 20) j + (0 - 8) k \\ = −6 i + 17 j - 8 k . \end{matrix}

Notice that this answer confirms the calculation of the cross product in [link] .

Got questions? Get instant answers now!

Use determinant notation to find $a \times b,$ where $a = ⟨ 8, 2, 3 ⟩$ and $b = ⟨ −1, 0, 4 ⟩ .$

$8 i - 35 j + 2 k$

Got questions? Get instant answers now!

Using the cross product

The cross product is very useful for several types of calculations, including finding a vector orthogonal to two given vectors, computing areas of triangles and parallelograms, and even determining the volume of the three-dimensional geometric shape made of parallelograms known as a parallelepiped . The following examples illustrate these calculations.

Finding a unit vector orthogonal to two given vectors

Let $a = ⟨ 5, 2, −1 ⟩$ and $b = ⟨ 0, −1, 4 ⟩ .$ Find a unit vector orthogonal to both $a$ and $b .$

The cross product $a \times b$ is orthogonal to both vectors $a$ and $b .$ We can calculate it with a determinant:

\begin{matrix} a \times b & = | \begin{matrix} i & j & k \\ 5 & 2 & −1 \\ 0 & −1 & 4 \end{matrix} | = | \begin{matrix} 2 & −1 \\ −1 & 4 \end{matrix} | i - | \begin{matrix} 5 & −1 \\ 0 & 4 \end{matrix} | j + | \begin{matrix} 5 & 2 \\ 0 & −1 \end{matrix} | k \\ = (8 - 1) i - (20 - 0) j + (−5 - 0) k \\ = 7 i - 20 j - 5 k . \end{matrix}

Normalize this vector to find a unit vector in the same direction:

‖ a \times b ‖ = \sqrt{{(7)}^{2} + {(−20)}^{2} + {(−5)}^{2}} = \sqrt{474} .

Thus, $⟨ \frac{7}{\sqrt{474}}, \frac{−20}{\sqrt{474}}, \frac{−5}{\sqrt{474}} ⟩$ is a unit vector orthogonal to $a$ and $b .$

Got questions? Get instant answers now!

Find a unit vector orthogonal to both $a$ and $b,$ where $a = ⟨ 4, 0, 3 ⟩$ and $b = ⟨ 1, 1, 4 ⟩ .$

$⟨ \frac{−3}{\sqrt{194}}, \frac{−13}{\sqrt{194}}, \frac{4}{\sqrt{194}} ⟩$

Got questions? Get instant answers now!

To use the cross product for calculating areas, we state and prove the following theorem.

Area of a parallelogram

If we locate vectors $u$ and $v$ such that they form adjacent sides of a parallelogram, then the area of the parallelogram is given by $‖ u \times v ‖$ ( [link] ).

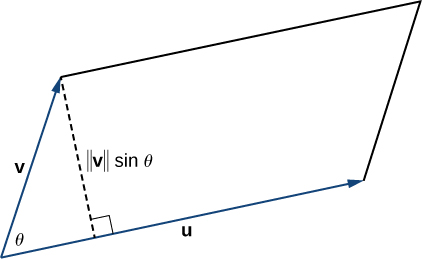
This figure is a parallelogram. One side is represented with a vector labeled “v.” The second side, the base, has the same initial point as vector v and is labeled “u.” The angle between u and v is theta. Also, a perpendicular line segment is drawn from the terminal point of v to vector u. It is labeled “|v|sin(theta).” — The parallelogram with adjacent sides $u$ and $v$ has base $‖ u ‖$ and height $‖ v ‖ sin θ .$

Proof

We show that the magnitude of the cross product is equal to the base times height of the parallelogram.

\begin{matrix} Area of a parallelogram & = base \times height \\ = ‖ u ‖ (‖ v ‖ sin θ) \\ = ‖ u \times v ‖ \end{matrix}

□

Finding the area of a triangle

Let $P = (1, 0, 0), Q = (0, 1, 0), and R = (0, 0, 1)$ be the vertices of a triangle ( [link] ). Find its area.

This figure is the 3-dimensional coordinate system. It has a triangle drawn in the first octant. The vertices of the triangle are points P(1, 0, 0); Q(0, 1, 0); and R(0, 0, 1). — Finding the area of a triangle by using the cross product.

We have $\vec{P Q} = ⟨ 0 - 1, 1 - 0, 0 - 0 ⟩ = ⟨ −1, 1, 0 ⟩$ and $\vec{P R} = ⟨ 0 - 1, 0 - 0, 1 - 0 ⟩ = ⟨ −1, 0, 1 ⟩ .$ The area of the parallelogram with adjacent sides $\vec{P Q}$ and $\vec{P R}$ is given by $‖ \vec{P Q} \times \vec{P R} ‖ :$

\begin{matrix} \vec{P Q} \times \vec{P R} & = & | \begin{matrix} i & j & k \\ −1 & 1 & 0 \\ −1 & 0 & 1 \end{matrix} | = (1 - 0) i - (−1 - 0) j + (0 - (−1)) k = i + j + k \\ ‖ \vec{P Q} \times \vec{P R} ‖ & = & ‖ ⟨ 1, 1, 1 ⟩ ‖ = \sqrt{1^{2} + 1^{2} + 1^{2}} = \sqrt{3} . \end{matrix}

The area of $Δ P Q R$ is half the area of the parallelogram, or $\sqrt{3} / 2 .$

Got questions? Get instant answers now!

Find the area of the parallelogram $P Q R S$ with vertices $P (1, 1, 0), Q (7, 1, 0), R (9, 4, 2),$ and $S (3, 4, 2) .$

$6 \sqrt{13}$

Got questions? Get instant answers now!

Questions & Answers

how did the oxygen help a human being

Achol Reply

how did the nutrition help the plants

Achol Reply

Biology is a branch of Natural science which deals/About living Organism.

Ahmedin Reply

what is phylogeny

Odigie Reply

evolutionary history and relationship of an organism or group of organisms

AI-Robot

Deng

what is biology

Hajah Reply

cell is the smallest unit of the humanity biologically

Abraham

what is biology

Victoria Reply

what is biology

Abraham

HOW CAN MAN ORGAN FUNCTION

Alfred Reply

the diagram of the digestive system

Assiatu Reply

allimentary cannel

Ogenrwot

How does twins formed

William Reply

They formed in two ways first when one sperm and one egg are splited by mitosis or two sperm and two eggs join together

Oluwatobi

what is genetics

Josephine Reply

Genetics is the study of heredity

Misack

how does twins formed?

Misack

What is manual

Hassan Reply

discuss biological phenomenon and provide pieces of evidence to show that it was responsible for the formation of eukaryotic organelles

Joseph Reply

what is biology

Yousuf Reply

the study of living organisms and their interactions with one another and their environment.

Wine

discuss the biological phenomenon and provide pieces of evidence to show that it was responsible for the formation of eukaryotic organelles in an essay form

Joseph Reply

what is the blood cells

Shaker Reply

list any five characteristics of the blood cells

Shaker

Got questions? Join the online conversation and get instant answers!

Jobilize.com Reply

<< Chapter < Page Page > Chapter >>

Practice Key Terms 6

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Calculus volume 3. OpenStax CNX. Feb 05, 2016 Download for free at http://legacy.cnx.org/content/col11966/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?

Ask

	13 AP 13 Nervous System Essay By OpenStax Start Flashcards
©flickr: Gage	How well do you know Ross Lynch? By Brianna Beck Start Quiz
	Does your crush like you? By Hoy Wen Start Quiz
	Socialism Command Economy By Robert Murphy Start Test
	15 Dr. Amberg Pharm quiz By Brooke Delaney Start Exam
©flickr: Iqbal	Liver Cancer By Darlene Paliswat Start Test
	3 Sociology 03 Culture MCQ By OpenStax Start Quiz
	Chemistry Final By Briana Hamilton Start Flashcards
©flickr:	Dairy Cattle Evaluation Exam By Katy Keilers Start Exam
	37 Biology 37 The Endocrine System MCQ By OpenStax Start Quiz

2.4 The cross product (Page 4/16)

Using expansion along the first row to compute a 3 × 3 Determinant

Rule: cross product calculated by a determinant

Using determinant notation to find p × q

Using the cross product

Finding a unit vector orthogonal to two given vectors

Area of a parallelogram

Proof

Finding the area of a triangle

Questions & Answers

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Using expansion along the first row to compute a $3 \times 3$ Determinant

Using determinant notation to find $p \times q$