This module is from Elementary Algebra by Denny Burzynski and Wade Ellis, Jr.
Beginning with the graphical solution of systems, this chapter includes an interpretation of independent, inconsistent, and dependent systems and examples to illustrate the applications for these systems. The substitution method and the addition method of solving a system by elimination are explained, noting when to use each method. The five-step method is again used to illustrate the solutions of value and rate problems (coin and mixture problems), using drawings that correspond to the actual situation.Objectives of this module: become more familiar with the five-step method for solving applied problems, be able to solve number problems, be able to solve value and rate problems.
Overview
- The Five-Step Method
- Number Problems
- Value and Rate Problems: Coin Problems Problems and Mixture Problems
The five-step method
When solving practical problems, it is often more convenient to introduce two variables rather than only one. Two variables should be introduced only when two relationships can be found within the problem. Each relationship will produce an equation, and a system of two equations in two variables will result.
We will use the five-step method to solve these problems.
- Introduce two variables, one for each unknown quantity.
- Look for two relationships within the problem. Translate the verbal phrases into mathematical expressions to form two equations.
- Solve the resulting system of equations.
- Check the solution.
- Write a conclusion.
Sample set a (number problems)
The sum of two numbers is 37. One number is 5 larger than the other. What are the numbers?
Step 2: There are two relationships.
(a) The Sum is 37.
(b) One is 5 larger than the other.
Step 3:
We can easily solve this system by substitution. Substitute
for
in equation 1.
Step 4: The Sum is 37.
One is 5 larger than the other.
Step 5: The two numbers are 16 and 21.
Got questions? Get instant answers now!
Practice set a
The difference of two numbers is 9, and the sum of the same two numbers is 19. What are the two numbers?
Value and rate problems: coin problems problems and mixture problems
The problems in Sample Sets B and C are
value problems . They are referred to as value problems because one of the equations of the system used in solving them is generated by considering a
value, or rate, or amount times a quantity .
Sample set b (coin problems)
A parking meter contains 27 coins consisting only of dimes and quarters. If the meter contains $4.35, how many of each type of coin is there?
Step 2: There are two relationships.
(a) There are 27 coins.
(b) Contribution due to dimes =
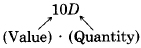
Contribution due to quarters =
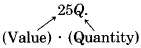
Step 3:
We can solve this system using elimination by addition. Multiply both sides of equation
by
and add.
Step 4: 16 dimes and 11 quarters is 27 coins.
The solution checks.
Step 5: There are 11 quarters and 16 dimes.
Got questions? Get instant answers now!
![]()
![]()
