| << Chapter < Page | Chapter >> Page > |
Solve the system
Step 1: Solve equation 1 for
Step 2: Substitute the expression
for
into equation 2.
Step 3: Solve the equation obtained in step 2.
Computations have eliminated all the variables and produce a contradiction. These lines are parallel.
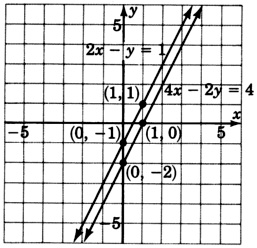
This system is inconsistent.
Slove the system
Substitution produces or , a contradiction. These lines are parallel and the system is inconsistent.
The following rule alerts us to the fact that the two lines of a system are coincident.
Solve the system
Step 1: Divide equation 1 by 4 and solve for
Step 2: Substitute the expression
for
in equation 2.
Step 3: Solve the equation obtained in step 2.
Computations have eliminated all the variables and produced an identity. These lines are coincident.
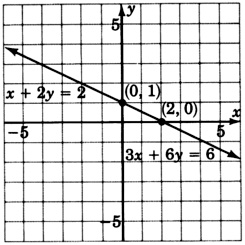
This system is dependent.
Solve the system
Computations produce an identity. These lines are coincident and the system is dependent.
Systems in which a coefficient of one of the variables is not 1 or cannot be made to be 1 without introducing fractions are not well suited for the substitution method. The problem in Sample Set D illustrates this “messy” situation.
Solve the system
Step 1: We will solve equation
for
Step 2: Substitute the expression
for
in equation
Step 3: Solve the equation obtained in step 2.
Step 4: Substitute
into the equation obtained in step
We now have
and
Step 5: Substitution will show that these values of
and
check.
Step 6: The solution is
For the following problems, solve the systems by substitution.
( [link] ) Find the difference:
( [link] ) Use the quadratic formula to solve

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?