This module is from Elementary Algebra by Denny Burzynski and Wade Ellis, Jr.
Factoring is an essential skill for success in algebra and higher level mathematics courses. Therefore, we have taken great care in developing the student's understanding of the factorization process. The technique is consistently illustrated by displaying an empty set of parentheses and describing the thought process used to discover the terms that are to be placed inside the parentheses.The factoring scheme for special products is presented with both verbal and symbolic descriptions, since not all students can interpret symbolic descriptions alone. Two techniques, the standard "trial and error" method, and the "collect and discard" method (a method similar to the "ac" method), are presented for factoring trinomials with leading coefficients different from 1.
Objectives of this module: be able to factor a monomial from a polynomial.
Overview
- The Factorization Process
The factorization process
We introduce the process of factoring a monomial from a polynomial by examining a problem: Suppose that
is the product and one of the factors is
.
To find the other factor we could set up the problem this way:
Since the product
consists of two terms, the expression multiplying
must consist of two terms, since, by the distributive property
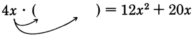
Now we see that this problem is simply an extension of finding the factors of a monomial.
Thus,
.
Usually, these divisions can be done mentally and the terms of the factor filled in directly.
Sample set a
The product is
and one factor is
.
Find the other factor.
We have the problem:
times "what expression" yields
? Mathematically,
Since there are four terms in the product, there must be four terms inside the parentheses. To find each of the four terms, we’ll divide (mentally) each term of the product by
.
The resulting quotient will be the necessary term of the factor.
Therefore, the other factor is
.
This result can be checked by applying the distributive property.
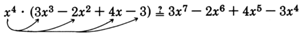
Thus,
Again, if the divisions can be performed mentally, the process can proceed very quickly.
The product is
and a factor is
. Find the other factor.
Since there are three terms in the product, there must be three terms inside the parentheses. To find each of these three terms, we’ll divide each term of the product by
.
The other factor is
, and
The product is
and a factor is
. Find the other factor.
Since there are three terms in the product, there must be three terms inside the parentheses. We will divide (mentally) each term of the product by
.
The other factor is
, and
Without writing the
, we get
The product is
and a factor is
. Find the other factor.
Mentally dividing each term of the original trinomial by
, we get
as the other factor, and
Practice set a
The product is
and a factor is
. Find the other factor.
The product is
and a factor is
. Find the other factor.
The product is
and a factor is
. Find the other factor.
The product is
and a factor is
. Find the other factor.
The product is
and a factor is
. Find the other factor.
Exercises
For the following problems, the first quantity represents the product and the second quantity a factor. Find the other factor.
Exercises for review
(
[link] ) How many
’s are there in
?
(
[link] ) Find the product.
.
(
[link] ) Solve
.
(
[link] ) Given that
is a factor of
, find the other factor.
![]()
![]()
