4.5 Derivatives and the shape of a graph  (Page 4/14)

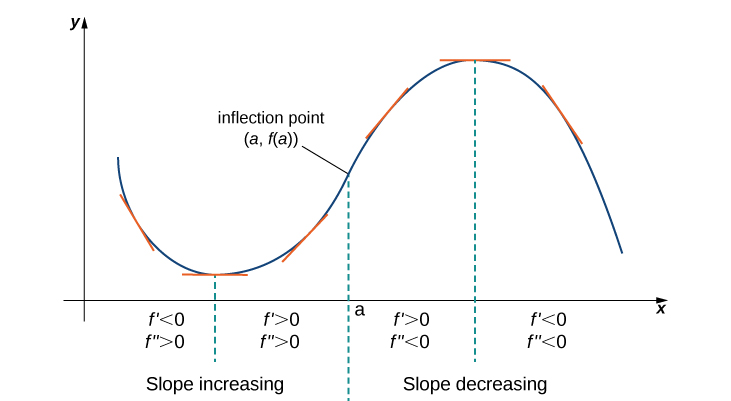
We conclude that we can determine the concavity of a function $f$ by looking at the second derivative of $f.$ In addition, we observe that a function $f$ can switch concavity ( [link] ). However, a continuous function can switch concavity only at a point $x$ if $f\text{″}\left(x\right)=0$ or $f\text{″}\left(x\right)$ is undefined. Consequently, to determine the intervals where a function $f$ is concave up and concave down, we look for those values of $x$ where $f\text{″}\left(x\right)=0$ or $f\text{″}\left(x\right)$ is undefined. When we have determined these points, we divide the domain of $f$ into smaller intervals and determine the sign of $f\text{″}$ over each of these smaller intervals. If $f\text{″}$ changes sign as we pass through a point $x,$ then $f$ changes concavity. It is important to remember that a function $f$ may not change concavity at a point $x$ even if $f\text{″}\left(x\right)=0$ or $f\text{″}\left(x\right)$ is undefined. If, however, $f$ does change concavity at a point $a$ and $f$ is continuous at $a,$ we say the point $\left(a,f\left(a\right)\right)$ is an inflection point of $f.$

Testing for concavity

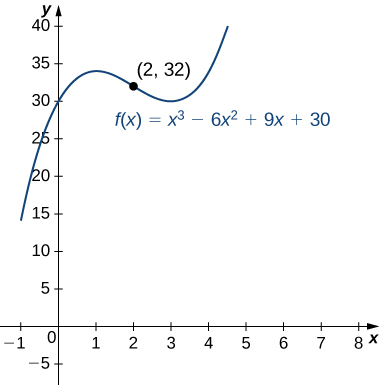
For the function $f\left(x\right)=x^3-6x^2+9x+30,$ determine all intervals where $f$ is concave up and all intervals where $f$ is concave down. List all inflection points for $f.$ Use a graphing utility to confirm your results.

To determine concavity, we need to find the second derivative $f\text{″}\left(x\right).$ The first derivative is $f\prime \left(x\right)=3x^2-12x+9,$ so the second derivative is $f\text{″}\left(x\right)=6x-12.$ If the function changes concavity, it occurs either when $f\text{″}\left(x\right)=0$ or $f\text{″}\left(x\right)$ is undefined. Since $f\text{″}$ is defined for all real numbers $x,$ we need only find where $f\text{″}\left(x\right)=0.$ Solving the equation $6x-12=0,$ we see that $x=2$ is the only place where $f$ could change concavity. We now test points over the intervals $\left(\text{−}\infty ,2\right)$ and $\left(2,\infty \right)$ to determine the concavity of $f.$ The points $x=0$ and $x=3$ are test points for these intervals.

Interval	Test Point	Sign of $f\text{″}\left(x\right)=6x-12$ at Test Point	Conclusion
$\left(\text{−}\infty ,2\right)$	$x=0$	$-$	$f$ is concave down
$\left(2,\infty \right)$	$x=3$	$+$	$f$ is concave up.

We conclude that $f$ is concave down over the interval $\left(\text{−}\infty ,2\right)$ and concave up over the interval $\left(2,\infty \right).$ Since $f$ changes concavity at $x=2,$ the point $\left(2,f\left(2\right)\right)=\left(2,32\right)$ is an inflection point. [link] confirms the analytical results.

Got questions? Get instant answers now!

Got questions? Get instant answers now!

We now summarize, in [link] , the information that the first and second derivatives of a function $f$ provide about the graph of $f,$ and illustrate this information in [link] .