| << Chapter < Page | Chapter >> Page > |
For the following exercises, determine whether the graph of the function provided is a graph of a polynomial function. If so, determine the number of turning points and the least possible degree for the function.
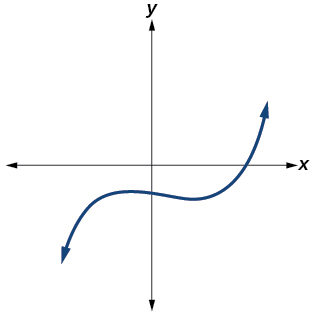
Yes. Number of turning points is 2. Least possible degree is 3.
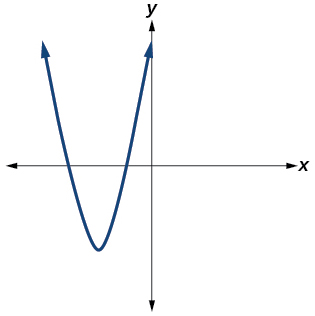
Yes. Number of turning points is 1. Least possible degree is 2.
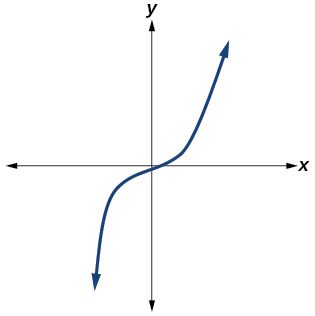
Yes. Number of turning points is 0. Least possible degree is 1.
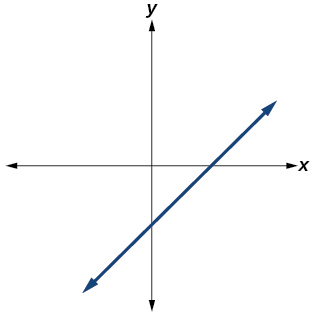
Yes. Number of turning points is 0. Least possible degree is 1.
For the following exercises, make a table to confirm the end behavior of the function.
For the following exercises, graph the polynomial functions using a calculator. Based on the graph, determine the intercepts and the end behavior.
For the following exercises, use the information about the graph of a polynomial function to determine the function. Assume the leading coefficient is 1 or –1. There may be more than one correct answer.
The intercept is The intercepts are Degree is 2.
End behavior:
The intercept is The intercepts are Degree is 2.
End behavior:
The intercept is The intercepts are Degree is 3.
End behavior:
The intercept is The intercept is Degree is 3.
End behavior:
The intercept is There is no intercept. Degree is 4.
End behavior:
For the following exercises, use the written statements to construct a polynomial function that represents the required information.
An oil slick is expanding as a circle. The radius of the circle is increasing at the rate of 20 meters per day. Express the area of the circle as a function of the number of days elapsed.
A cube has an edge of 3 feet. The edge is increasing at the rate of 2 feet per minute. Express the volume of the cube as a function of the number of minutes elapsed.
A rectangle has a length of 10 inches and a width of 6 inches. If the length is increased by inches and the width increased by twice that amount, express the area of the rectangle as a function of
An open box is to be constructed by cutting out square corners of inch sides from a piece of cardboard 8 inches by 8 inches and then folding up the sides. Express the volume of the box as a function of
A rectangle is twice as long as it is wide. Squares of side 2 feet are cut out from each corner. Then the sides are folded up to make an open box. Express the volume of the box as a function of the width ( ).

Notification Switch
Would you like to follow the 'College algebra' conversation and receive update notifications?