| << Chapter < Page | Chapter >> Page > |
Access this online resource for additional instruction and practice with rates of change.
| Average rate of change |
Can the average rate of change of a function be constant?
Yes, the average rate of change of all linear functions is constant.
If a function is increasing on and decreasing on then what can be said about the local extremum of on
How are the absolute maximum and minimum similar to and different from the local extrema?
The absolute maximum and minimum relate to the entire graph, whereas the local extrema relate only to a specific region around an open interval.
How does the graph of the absolute value function compare to the graph of the quadratic function, in terms of increasing and decreasing intervals?
For the following exercises, find the average rate of change of each function on the interval specified for real numbers or in simplest form.
For the following exercises, consider the graph of shown in [link] .
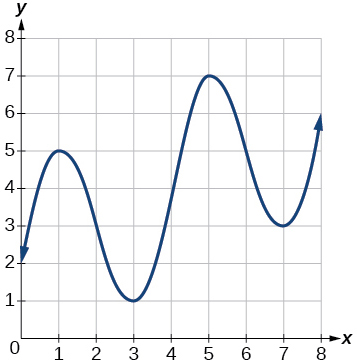
Estimate the average rate of change from to
For the following exercises, use the graph of each function to estimate the intervals on which the function is increasing or decreasing.
For the following exercises, consider the graph shown in [link] .

Notification Switch
Would you like to follow the 'College algebra' conversation and receive update notifications?