1. Home
  2. Calculus volume 3
  3. Multiple integration
  4. Triple integrals in cylindrical

5.5 Triple integrals in cylindrical and spherical coordinates  (Page 5/12)

<< Chapter < Page
  Calculus volume 3     Page 5 / 12
Chapter >> Page >

Now we can illustrate the following theorem for triple integrals in spherical coordinates with ( ρ i j k * , θ i j k * , φ i j k * ) being any sample point in the spherical subbox B i j k . For the volume element of the subbox Δ V in spherical coordinates, we have Δ V = ( Δ ρ ) ( ρ Δ φ ) ( ρ sin φ Δ θ ) , , as shown in the following figure.

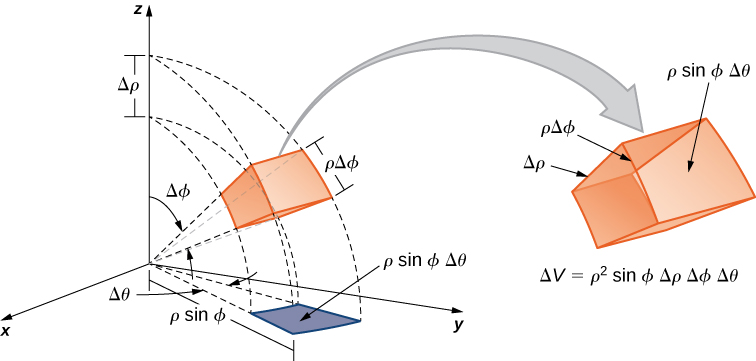
In the spherical coordinate space, a box is projected onto the polar coordinate plane. On the polar coordinate plane, the projection has area rho sin phi Delta theta. On the z axis, a distance Delta rho is indicated, and from these boundaries, angles are made that project through the edges of the box. There is also a blown up version of the box that shows it has sides Delta rho, rho Delta phi, and rho sin phi Delta theta, with overall volume Delta V = rho squared sin phi Delta rho Delta phi Delta theta.
The volume element of a box in spherical coordinates.

Definition

The triple integral in spherical coordinates    is the limit of a triple Riemann sum,

lim l , m , n → ∞ ∑ i = 1 l ∑ j = 1 m ∑ k = 1 n f ( ρ i j k * , θ i j k * , φ i j k * ) ( ρ i j k * ) 2 sin φ Δ ρ Δ θ Δ φ

provided the limit exists.

As with the other multiple integrals we have examined, all the properties work similarly for a triple integral in the spherical coordinate system, and so do the iterated integrals. Fubini’s theorem takes the following form.

Fubini’s theorem for spherical coordinates

If f ( ρ , θ , φ ) is continuous on a spherical solid box B = [ a , b ] × [ α , β ] × [ γ , ψ ] , then

∭ B f ( ρ , θ , φ ) ρ 2 sin φ d ρ d φ d θ = ∫ φ = γ φ = ψ ∫ θ = α θ = β ∫ ρ = a ρ = b f ( ρ , θ , φ ) ρ 2 sin φ d ρ d φ d θ .

This iterated integral may be replaced by other iterated integrals by integrating with respect to the three variables in other orders.

As stated before, spherical coordinate systems work well for solids that are symmetric around a point, such as spheres and cones. Let us look at some examples before we consider triple integrals in spherical coordinates on general spherical regions.

Evaluating a triple integral in spherical coordinates

Evaluate the iterated triple integral ∫ θ = 0 θ = 2 π ∫ φ = 0 φ = π / 2 ∫ p = 0 ρ = 1 ρ 2 sin φ d ρ d φ d θ .

As before, in this case the variables in the iterated integral are actually independent of each other and hence we can integrate each piece and multiply:

∫ 0 2 π ∫ 0 π / 2 ∫ 0 1 ρ 2 sin φ d ρ d φ d θ = ∫ 0 2 π d θ ∫ 0 π / 2 sin φ d φ ∫ 0 1 ρ 2 d ρ = ( 2 π ) ( 1 ) ( 1 3 ) = 2 π 3 .
Got questions? Get instant answers now!
Got questions? Get instant answers now!

The concept of triple integration in spherical coordinates can be extended to integration over a general solid, using the projections onto the coordinate planes. Note that d V and d A mean the increments in volume and area, respectively. The variables V and A are used as the variables for integration to express the integrals.

The triple integral of a continuous function f ( ρ , θ , φ ) over a general solid region

E = { ( ρ , θ , φ ) | ( ρ , θ ) ∈ D , u 1 ( ρ , θ ) ≤ φ ≤ u 2 ( ρ , θ ) }

in ℝ 3 , where D is the projection of E onto the ρ θ -plane, is

∭ E f ( ρ , θ , φ ) d V = ∬ D [ ∫ u 1 ( ρ , θ ) u 2 ( ρ , θ ) f ( ρ , θ , φ ) d φ ] d A .

In particular, if D = { ( ρ , θ ) | g 1 ( θ ) ≤ ρ ≤ g 2 ( θ ) , α ≤ θ ≤ β } , then we have

∭ E f ( ρ , θ , φ ) d V = ∫ α β ∫ g 1 ( θ ) g 2 ( θ ) ∫ u 1 ( ρ , θ ) u 2 ( ρ , θ ) f ( ρ , θ , φ ) ρ 2 sin φ d φ d ρ d θ .

Similar formulas occur for projections onto the other coordinate planes.

Setting up a triple integral in spherical coordinates

Set up an integral for the volume of the region bounded by the cone z = 3 ( x 2 + y 2 ) and the hemisphere z = 4 − x 2 − y 2 (see the figure below).

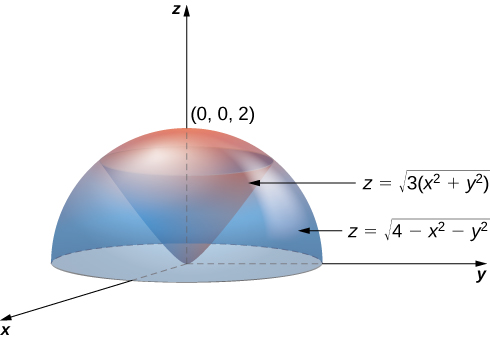
A hemisphere with equation z = the square root of (4 minus x squared minus y squared) in the upper half plane, and within it, a cone with equation z = the square root of (3 times (x squared + y squared)) that is pointing down, with vertex at the origin.
A region bounded below by a cone and above by a hemisphere.

Using the conversion formulas from rectangular coordinates to spherical coordinates, we have:

For the cone: z = 3 ( x 2 + y 2 ) or ρ cos φ = 3 ρ sin φ or tan φ = 1 3 or φ = π 6 .

For the sphere: z = 4 − x 2 − y 2 or z 2 + x 2 + y 2 = 4 or ρ 2 = 4 or ρ = 2 .

Thus, the triple integral for the volume is V ( E ) = ∫ θ = 0 θ = 2 π ∫ ϕ = 0 φ = π / 6 ∫ ρ = 0 ρ = 2 ρ 2 sin φ d ρ d φ d θ .

Got questions? Get instant answers now!
Got questions? Get instant answers now!

Set up a triple integral for the volume of the solid region bounded above by the sphere ρ = 2 and bounded below by the cone φ = π / 3 .

V ( E ) = ∫ θ = 0 θ = 2 π ∫ ϕ = 0 φ = π / 3 ∫ ρ = 0 ρ = 2 ρ 2 sin φ d ρ d φ d θ

Got questions? Get instant answers now!
<< Chapter < Page Page > Chapter >>
Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Calculus volume 3. OpenStax CNX. Feb 05, 2016 Download for free at http://legacy.cnx.org/content/col11966/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?

Ask