| << Chapter < Page | Chapter >> Page > |
Draw a free-body diagram to represent the forces acting on a kite on a string that is floating stationary in the air. Label the forces in your diagram.

The diagram has a black dot and three solid red arrows pointing away from the dot. Arrow Ft is long and pointing to the left and slightly down. Arrow Fw is also long and is a bit below a diagonal line halfway between pointing up and pointing to the right. A short arrow Fg is pointing down.
F g is the force on the kite due to gravity.
F w is the force exerted on the kite by the wind.
F t is the force of tension in the string holding the kite. It must balance the vector sum of the other two forces for the kite to float stationary in the air.
A car is sliding down a hill with a slope of 20°. The mass of the car is 965 kg. When a cable is used to pull the car up the slope, a force of 4215 N is applied. What is the car’s acceleration, ignoring friction?
If a leg is suspended by a traction setup as shown in [link] , what is the tension in the rope?
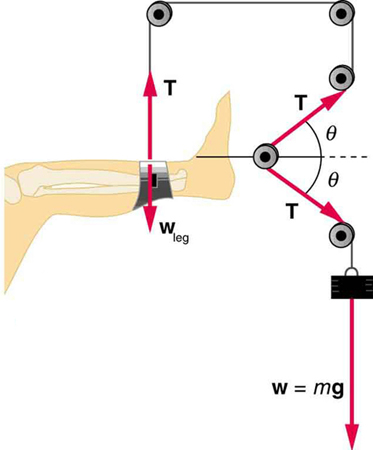
In a traction setup for a broken bone, with pulleys and rope available, how might we be able to increase the force along the tibia using the same weight? (See [link] .) (Note that the tibia is the shin bone shown in this image.)
Two teams of nine members each engage in a tug of war. Each of the first team’s members has an average mass of 68 kg and exerts an average force of 1350 N horizontally. Each of the second team’s members has an average mass of 73 kg and exerts an average force of 1365 N horizontally. (a) What is magnitude of the acceleration of the two teams? (b) What is the tension in the section of rope between the teams?
What force does a trampoline have to apply to a 45.0-kg gymnast to accelerate her straight up at ? Note that the answer is independent of the velocity of the gymnast—she can be moving either up or down, or be stationary.
(a) Calculate the tension in a vertical strand of spider web if a spider of mass hangs motionless on it. (b) Calculate the tension in a horizontal strand of spider web if the same spider sits motionless in the middle of it much like the tightrope walker in [link] . The strand sags at an angle of below the horizontal. Compare this with the tension in the vertical strand (find their ratio).
(a)
(b) . This is 2.41 times the tension in the vertical strand.
Suppose a 60.0-kg gymnast climbs a rope. (a) What is the tension in the rope if he climbs at a constant speed? (b) What is the tension in the rope if he accelerates upward at a rate of ?
Show that, as stated in the text, a force exerted on a flexible medium at its center and perpendicular to its length (such as on the tightrope wire in [link] ) gives rise to a tension of magnitude .
Newton’s second law applied in vertical direction gives
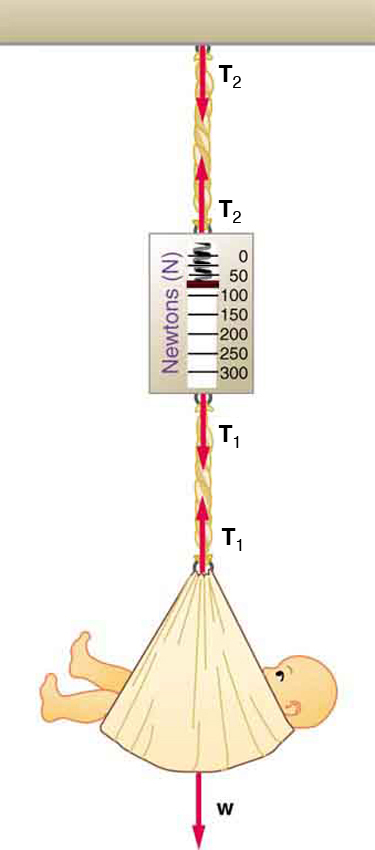
Consider the baby being weighed in [link] . (a) What is the mass of the child and basket if a scale reading of 55 N is observed? (b) What is the tension in the cord attaching the baby to the scale? (c) What is the tension in the cord attaching the scale to the ceiling, if the scale has a mass of 0.500 kg? (d) Draw a sketch of the situation indicating the system of interest used to solve each part. The masses of the cords are negligible.

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?