22.5 Force on a moving charge in a magnetic field: examples and

Learning objectives

By the end of this section, you will be able to:

• Describe the effects of a magnetic field on a moving charge.
• Calculate the radius of curvature of the path of a charge that is moving in a magnetic field.

The information presented in this section supports the following AP® learning objectives and science practices:

• 3.C.3.1 The student is able to use right-hand rules to analyze a situation involving a current-carrying conductor and a moving electrically charged object to determine the direction of the magnetic force exerted on the charged object due to the magnetic field created by the current-carrying conductor. (S.P. 1.4)

Magnetic force can cause a charged particle to move in a circular or spiral path. Cosmic rays are energetic charged particles in outer space, some of which approach the Earth. They can be forced into spiral paths by the Earth’s magnetic field. Protons in giant accelerators are kept in a circular path by magnetic force. The bubble chamber photograph in [link] shows charged particles moving in such curved paths. The curved paths of charged particles in magnetic fields are the basis of a number of phenomena and can even be used analytically, such as in a mass spectrometer.

So does the magnetic force cause circular motion? Magnetic force is always perpendicular to velocity, so that it does no work on the charged particle. The particle’s kinetic energy and speed thus remain constant. The direction of motion is affected, but not the speed. This is typical of uniform circular motion. The simplest case occurs when a charged particle moves perpendicular to a uniform $B$ -field, such as shown in [link] . (If this takes place in a vacuum, the magnetic field is the dominant factor determining the motion.) Here, the magnetic force supplies the centripetal force $F_{\mathrm{c}}={\text{mv}}^2/r$ . Noting that $\text{sin}\theta =1$ , we see that $F=\text{qvB}$ .

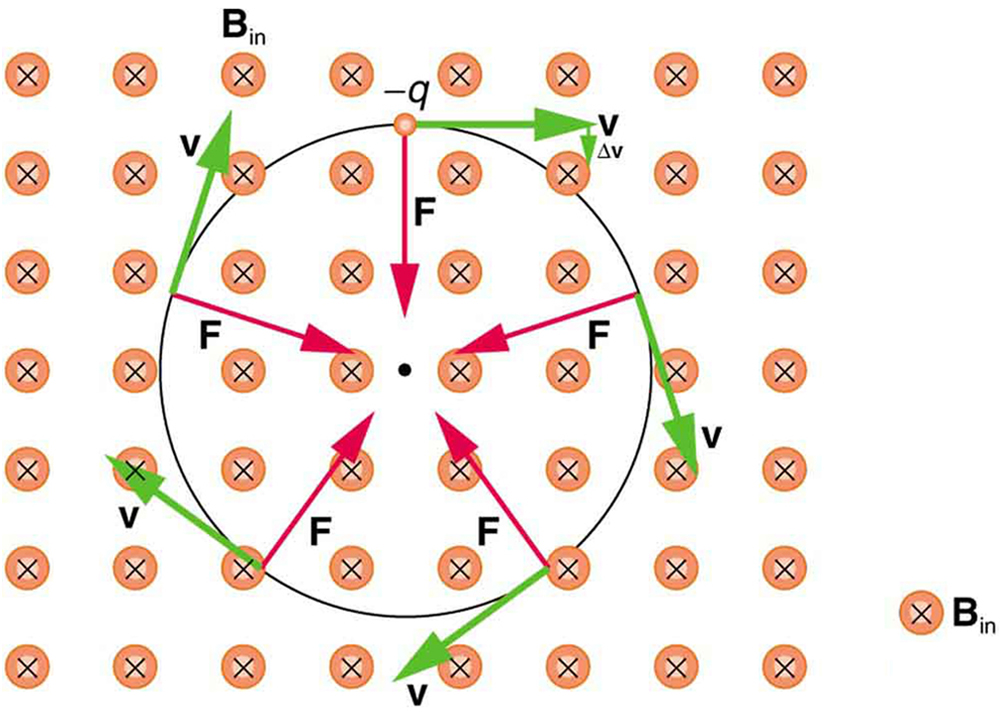
Because the magnetic force $F$ supplies the centripetal force $F_{\mathrm{c}}$ , we have

Solving for $r$ yields

Here, $r$ is the radius of curvature of the path of a charged particle with mass $m$ and charge $q$ , moving at a speed $v$ perpendicular to a magnetic field of strength $B$ . If the velocity is not perpendicular to the magnetic field, then $v$ is the component of the velocity perpendicular to the field. The component of the velocity parallel to the field is unaffected, since the magnetic force is zero for motion parallel to the field. This produces a spiral motion rather than a circular one.