| << Chapter < Page | Chapter >> Page > |
(a) Calculate the energy released by the fusion of a 1.00-kg mixture of deuterium and tritium, which produces helium. There are equal numbers of deuterium and tritium nuclei in the mixture.
(b) If this takes place continuously over a period of a year, what is the average power output?
Strategy
According to , the energy per reaction is 17.59 MeV. To find the total energy released, we must find the number of deuterium and tritium atoms in a kilogram. Deuterium has an atomic mass of about 2 and tritium has an atomic mass of about 3, for a total of about 5 g per mole of reactants or about 200 mol in 1.00 kg. To get a more precise figure, we will use the atomic masses from Appendix A. The power output is best expressed in watts, and so the energy output needs to be calculated in joules and then divided by the number of seconds in a year.
Solution for (a)
The atomic mass of deuterium ( ) is 2.014102 u, while that of tritium ( ) is 3.016049 u, for a total of 5.032151 u per reaction. So a mole of reactants has a mass of 5.03 g, and in 1.00 kg there are . The number of reactions that take place is therefore
The total energy output is the number of reactions times the energy per reaction:
Solution for (b)
Power is energy per unit time. One year has , so
Discussion
By now we expect nuclear processes to yield large amounts of energy, and we are not disappointed here. The energy output of from fusing 1.00 kg of deuterium and tritium is equivalent to 2.6 million gallons of gasoline and about eight times the energy output of the bomb that destroyed Hiroshima. Yet the average backyard swimming pool has about 6 kg of deuterium in it, so that fuel is plentiful if it can be utilized in a controlled manner. The average power output over a year is more than 10 MW, impressive but a bit small for a commercial power plant. About 32 times this power output would allow generation of 100 MW of electricity, assuming an efficiency of one-third in converting the fusion energy to electrical energy.
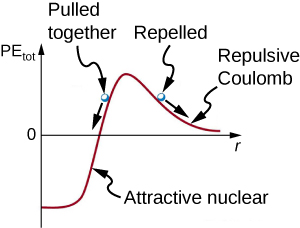
This figure shows a graph of the potential energy between two light nuclei as a function of the distance between them. Fusion can occur between the nuclei if the distance is
(c)
In a nuclear fusion reaction, 2 g of hydrogen is converted into 1.985 g of helium. What is the energy released?
When deuterium and tritium nuclei fuse to produce helium, what else is produced?
(d)
Suppose two deuterium nuclei are fused to produce helium.
Assume that the mass of deuterium is 2.014102 u, the mass of helium is 4.002603 u and 1 u = 1.66 × 10 -27 kg.

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?